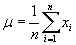
Average value is the arithmetic mean of a sequence of values.
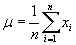
In Tolerance Analysis, where values are specific results of QuickFiels simulations, the average value is typically close to the nominal value (but for some problems and results it can differ).
Standard deviation is the root means square (RMS) of the difference between the random values and their average value.
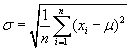
Standard deviation can be considered as the average deviation of the random values of some parameter from their average value.
It is often convenient also to use 3*σ as a measure of the deviation from the average value. For most cases, 3*σ is a good estimation for the maximum deviation. For more detail see Using 3*Sigma for Normal Distribution.
Normal distribution is a probability distribution with probability density function
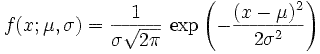
where μ is an average value and σ is a standard deviation.
Normal distribution is used very often in physics and engineering. As a rule, we can use the normal distribution model if we can assume that there are many small independent effects contributing to the result in an additive fashion.
In Tolerance Analysis, we use normal distribution both when we specify variations and when we analyze the statistics for results.
For variations, we generate the random variations using the normal distribution.
For results, we cannot be sure that the distribution is normal. However, in many practical cases it is so, especially when we specify many variations contributing to the result. So we calculate some statistical properties such as tolerance and the percent of defects assuming that the result distribution is normal.
If the distribution is not normal, the values for tolerance and percent of defects that Tolerance Analysis calculates can also be used, but typically as a rough estimation only.
In addition to the mean and the standard deviation, practically important characteristic of the normal distribution is 3*σ. The reason for it is that practically all (99.7%) the values for the normal distribution belong to the interval from μ - 3*σ to μ + 3*σ. (It can be easily observed at the plot, as we can see that at μ - 3*σ and μ + 3*σ points, the bell-shaped curve practically touches the X-axis).
So, for many practical applications 3*σ can be considered as a maximum deviation from the mean.
In Tolerance Analysis, we use 3*σ both for variations and for results.
For variations, 3*σ is the value that we specify when we fill in the form.
For example, we may specify that some label property can be changed by 1%. It actually means the following:
we will use normal distribution with σ = 0.33%
1% can be interpreted as the maximum deviation.
For results, we use 3*σ to calculate the tolerance and the tolerance limits. We calculate:
lower tolerance limit as μ - 3*σ
upper tolerance limit as μ + 3*σ
tolerance as the maximum distance between the nominal value and the upper and lower tolerance limits.
So, we can say if the distribution for the result value is normal or close to normal, then the tolerance limits define the range that contains practically all values.
If the distribution of the results is not normal, we can not guarantee the 99.7% percents. However the 3*σ is typically a reasonable estimation for maximum deviation, and tolerance and tolerance limits calculated by the formula described above can be used as an estimation for non-normal distributions as well.
The following facts about the precision of Monte Carlo method of the average and standard distribution calculations are useful:
To get the average and standard deviation with precision around 10% it is typically enough to have 30-50 runs.
To get considerably more precise values for average and standard deviation, it is typically necessary to have more then 1000 runs. For many practical applications it makes no sense, because 10% accuracy for tolerance is typically enough.
To get a relatively accurate histogram, it is necessary to have 100-200 runs or more. So we would reccomand to apply the following rule of thumb to the number of runs
selection:
Do the first calculation with a large number of runs (100-200) once to get an accurate histogram and to estimate whether the distribution is normal or close to normal.
If this hypothesis is true, you can run following calculations with 30-50 runs. Precision of results will be around 10% but for most practical goals it will be enough. Tip. To get more information about the theory beyond the Tolerance Analysis you can start reading from Wikipedia articles: Standard Deviation and Normal Distribution
For more information please see
Number of Runs and Precision of Results
Tolerance Analysis Main Features