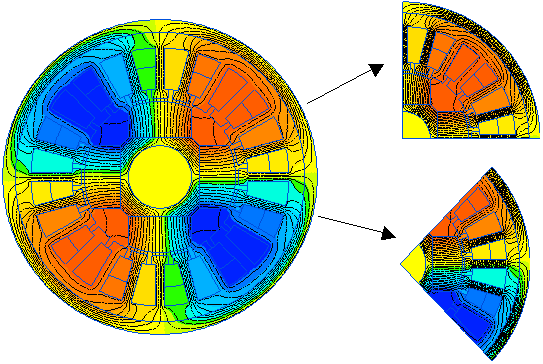
A special type of boundary conditions is implemented in QuickField to reduce the model size when simulating periodic structures, like poles in electric machines, - periodic boundary conditions. These conditions apply to two opposite sides of a model and force the fields on both boundaries to be either the same (even periodicity) or opposite (odd periodicity). The periodic condition is more generic than Dirichlet or Neumann condition, since it does not imply that the field is symmetric (no normal component) or antisymmetric (no tangential field) on the given boundary. Both components may exist, but they are forced to be the same or opposite.

Unlike other finite element packages, QuickField does not require that the mesh be equal on both boundaries, and is capable of merging potential values on edges with mismatching edge mesh.
To apply this type of condition, simply check the correspondent box (Even or Odd Periodical) for the label assigned to edges on the two boundaries - QuickField will analyze the geometry and detect the periodicity automatically.
Note:
If you expect symmetric or antisymmetric field behavior, even though the structure is periodic, it is still more efficient to apply Dirichlet or Neumann boundary condition.