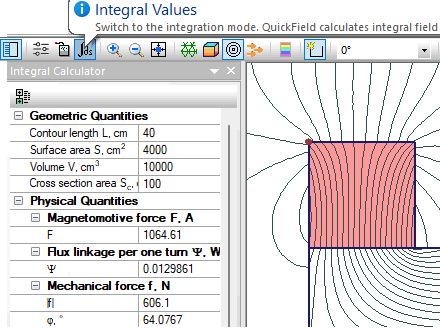
To calculate integrals, choose Integral Values in View menu. If the contour is already defined, a list of available integral quantities appears. The list varies depends on whether your contour is open or closed. If you have no contour defined in the active field view, a message appears prompting you to build the contour.
In plane-parallel problem, a contour defines cylindrical (in generalized sense) surface of infinite depth, or volume of that cylinder for volume integral. Therefore, in plane-parallel formulation surface and volume integrals are calculated per unit depth.
In axisymmetric problem, a contour defines toroidal surface, or toroid for volume integral.
Positive direction of a contour is counter-clockwise. The direction of the contour is accounted as follows:

Force, torque and electric charge integrals represent real physical quantities only when the contour is closed. However, these integrals are calculated for the unclosed contours too, for particular interest.
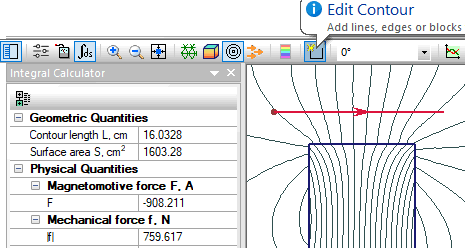
When the electrostatic or magnetic force, torque, electric charge, electric current or heat flux are to be calculated, the domain of integration may be chosen by many different ways. The only requirement for the surface of integration is to contain all the necessary bodies, but to avoid any extra bodies or field sources. It is important to understand that the accuracy will be the best if you choose the integration surface as far as possible from the places with strong inhomogeneity of field, e.g., field sources or boundaries of conducting or ferromagnetic bodies.
When calculating the flux linkage the domain of integration must exactly fit the cross section of the coil.