Coupled problems

QuickField is capable of importing loads (distributed sources) calculated in some problem into the problem of another type. Following coupling types are supported:

• Heat transfer caused by Joule heat generated in the DC or AC conduction or AC or transient magnetic problem.
• Thermal stresses based on a calculated temperature distribution.
• Stress analysis of the system loaded by magnetic or electric forces.
• Importing remembered magnetic state of soft magnetic materials.
• AC magnetic calculation taking into account temperature dependency of electrical conductivity.
• A special case of coupling allows for importing of the field distribution in some steady state or transient problem into another transient problem as its initial state. This applies to transient magnetic and transient heat transfer analysis.

In addition to imported loads, you can define any other loads and boundary conditions, similar to non-coupled problem.

You can combine several coupling types in one problem. E.g., after calculating currents distribution, electrostatic and magnetic fields as separate problems based on the same model file, you can calculate temperature distribution from Joule heat and then find stresses caused by temperature and magnetic and electric forces at once. However, such problems are rather rare.

Further we will call the problem, from which the data are being loaded, the source problem, and the problem, which imports the data, the target problem.

There are several rules to follow with coupled problems:

• Both source and target problem must share a single model file.
• Both problems must use the same formulation (plane or axisymmetric).
• Source problem must be up-to-date when solving the target problem.

Note. In spite of the requirement that coupled problems must use the same model file, the geometrical region for the problems need not coincide, i.e. some subregions those are in use in one problem, could be excluded from consideration in the other one.

Importing Joule Heat to Heat Transfer Problem

While importing data from DC or AC conduction problem to heat transfer one, heat sources due to Joule law are assumed in all subregions included into consideration in both source and target problems. In transient or AC magnetic problems, Joule heat is generated in all conductors. When importing Joule heat from transient magnetic problem into transient heat transfer, both processes are assumed to run synchronously. With this feature, you can simulate time-dependent heat distribution arising from time-dependent electric current distribution (including eddy currents) in a magnetic device.

Importing temperature distribution to stress analysis problem

While calculating thermal stresses, initial strains are assumed in all subregions, which are included into consideration in both problems and possess nonzero value of thermal expansion coefficient (or at least one of its components in anisotropic case). While importing the temperature distribution from the transient problem, you can choose the moment of time, the state at which you wish to import.

Importing magnetic forces to stress analysis problem

While importing magnetic force to stress analysis problem:

• Body force is assumed in all subregions included into consideration in both source and target problems, if those subregions have nonlinear magnetic properties and/or current density is defined (Lorentz force).
• Surface force is assumed at the boundaries separating subregions with different magnetic properties, boundaries with surface current, or outward boundaries in sense of magnetic problem. The surface force is also generated in the cases, when only one subregion, say, to the left of the boundary is active in sense of magnetic problem, and only the subregion to the right of it is active in stress analysis problem.

While importing the magnetic forces from the transient problem, you choose the moment of time, the state at which you wish to import.

Importing electric forces to stress analysis problem

While importing electric force to stress analysis problem:

• Body force is assumed for all subregions included into consideration in both source and target problems and carrying distributed charge density.
• Surface force is assumed at the boundaries separating subregions with different permittivity, boundaries with surface charge, or outward boundaries in sense of electric problem. The surface force is also generated in the cases, when only one subregion, say, to the left of the boundary is active in sense of electric problem, and only the subregion to the right of it is active in stress analysis problem.

Importing Magnetic State to DC or AC Magnetic problem

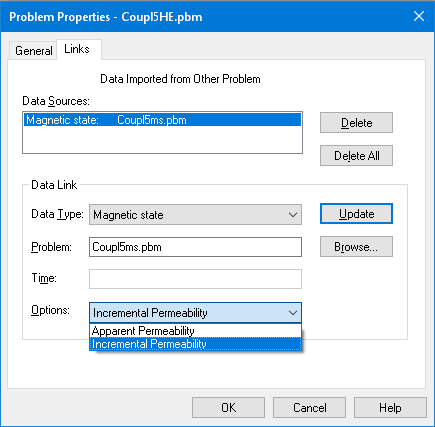
QuickField is able to remember the magnetic state of the media in the source problem for further use in target problems, where it is necessary to take into account the actual magnetic saturation.
Quantity, transferred from DC Magnetic problem is the value of magnetic permeability, calculated in every finite element of the source problem.

• In non-linear materials the remembered value of magnetic permeability is calculated using the magnetic flux density in the source problem;
• In linear materials the remembered value of magnetic permeability is taken from the corresponding block label properties of the source problem.

Taking into account that there are two types of magnetic permeability - apparent (static) and incremental (differential), the import dialog has a switch for selecting proper type of imported parameters. It should be mentioned that the choice between apparent and incremental permeability for importing depends on the application.

Fig. Magnetic import dialog.

Target problem will become linear, and the magnetic permeability values entered into the target problem description will be ignored and replaced by imported data. Magnetic state remembering is equivalent to the working point fixation for magnetic system.
This gives the possibility to calculate the differential mutual and self-inductances of multi-coil system in the target problems, by calculating the magnetic flux induced by current in only one of coils at time.

Importing Temperature Field to AC Magnetic Problem

QuickField allows importing the calculated temperature field into a problem of AC magnetics. This temperature field may be then used for calculating the values of the electrical conductivity for materials where the conductivity is temperature-dependent.

Related Topics
Coupled (Multiphysics) Examples