Formulations in Stress analysis

Within QuickField package, the plane stress, the plane strain and the axisymmetric stress models are available with both isotropic and orthotropic materials. The plane stress model is suitable for analyzing structures that are thin in the out-of-plane direction, e.g., thin plates subject to in-plate loading. Out-of-plane direct stress and shear stresses are assumed to be negligible. The plane strain model is formulated by assuming that out-of-plane strains are negligible. This model is suitable for structures that are thick in the out-of-plane direction.

Displacement, Strain and Stress

The displacement field is assumed to be completely defined by the two components of the displacement vector δ in each point:

{δ} =		- for plane problems;
{δ} =		- for axisymmetric problems.

Only three components of strain and stress tensors are independent in both plane stress and plane strain cases. The strain-displacement relationship is defined as:

{ε} =

=

.

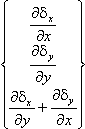
The corresponding stress components:

{σ} =

.

The axisymmetric problem formulation also includes the out-of-plane direct strain ε_θ, caused by the radial deformation. The strain-displacement relationship is defined as:

{ε} =

=

.

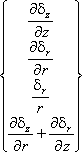
The corresponding stress components:

{σ} =

.

The equilibrium equations for the plane problems are:

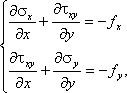
and for the axisymmetric problems are:

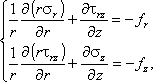
where f_x, f_y and f_z, f_r are components of the volume force vector.

For linear elasticity, the stresses are related to the strains using relationship of the form

{σ} = [D]({ε} - {ε₀}),

where D is a matrix of elastic constants, and ε₀ is the initial thermal strain. The specific form of the matrix depends on a particular problem formulation.

For plane stress and isotropic material:

[D] =

.

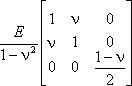
For plane stress and orthotropic material:

[D] =

.

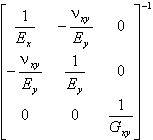
For plane strain and isotropic material:

[D] =

.

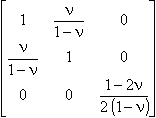
For plane strain and orthotropic material:

[D] =

.

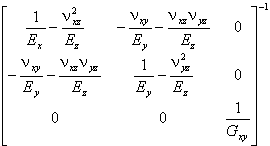
For axisymmetric problem and isotropic material:

[D] =

.

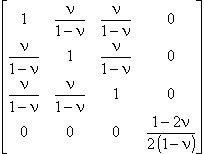
For axisymmetric problem and orthotropic material:

[D] =

.

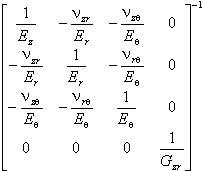
In all these equations E denotes Young's modulus of the isotropic material; E_x, E_y, E_z, E_r, and E_θ are the Young's moduli of the orthotropic material along the corresponding axes; ν is a Poisson's ratio for isotropic material; ν_yx, ν_zx, ν_zy, νrz, ν_θz, ν_θr are the Poisson's ratios for orthotropic material; G_xy and G_zr are the shear moduli.