Conducting sphere inside capacitor

QuickField simulation example

An uncharged conductive sphere is placed inside a charged parallel plate capacitor.

Problem Type
Axisymmetric problem of electrostatics

Geometry

Given
Sphere radius: R = 1 mm;
Distance between the plates: d = 10 mm;
Dielectric permittivity: ε = 4;
Plate size: A = 100x100 mm²;
Voltage applied: V+ = 24 V.

Task
Find the electric field stress in the dielectric.

Solution
To overcome 3D import limitations (only single body topology is allowed) we subtract the sphere from the dielectric body and import the resulting single body.
This problem could be simulated in 2D axisymmetric formulation if we replace square plates with discs of the same area (πD²/4 = A).
This modification preserves the inner field strength and the geometric capacitance values (~A/d).

To model the conducting body with unknown potential we set the electric permittivity to a very high value (10000). This effectively makes the body's surface equipotential (as the real conductor' surface would be).

Results
Analytical solution:
External uniform electric field E_0x = U / d = 24/10 = 2.4 [V/mm] = 2400 [V/m].
Electric potential outside the sphere U(x) = E_0x * (R³/x² - x) [V] *

Electric field distribution inside the dielectric:

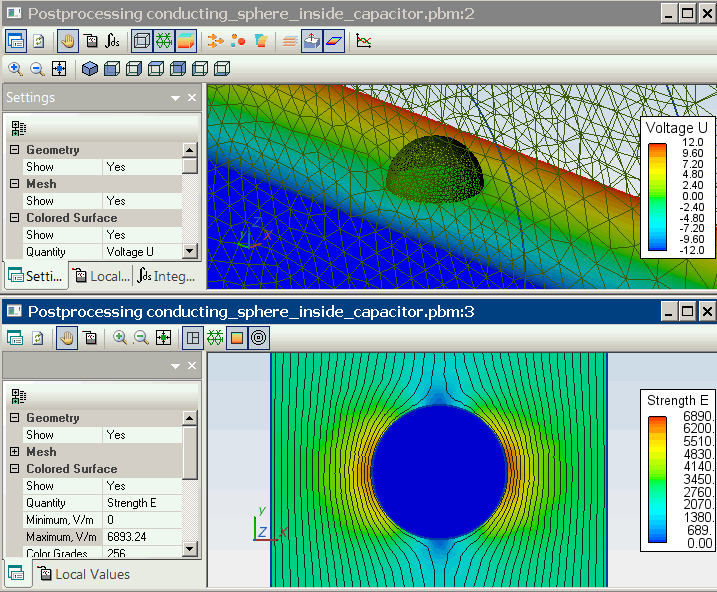
Electric potential distribution inside the dielectric:

*Reference: Haus, Hermann A., and James R. Melcher. Electromagnetic Fields and Energy. Englewood Cliffs, NJ: Prentice-Hall, 1989. ISBN: 9780132490207.

• Video: Conducting sphere inside capacitor. Watch on YouTube
  
• Download simulation files (files may be viewed using any QuickField Edition).