Conductive cylinder in rotating magnetic field

QuickField simulation example

Problem Type
Plane-parallel problem of transient magnetics.

Geometry

Given
Copper conductivity σ = 63 MS/m;
Magnitude of external field B₀ = 1 T;
Number of poles 2p = 6;
Frequency f = 50 Hz.

Solution
To specify rotating magnetic field on the outer boundary of the region, B_n = B₀ cos(pφ + ωt), we apply the Dirichlet boundary condition, using the formula:
A = (1/60) * cos(3*phi + 360*50*t).

The coefficient A₀ = 1/60 arises from consideration
B = rot A
B_n = (1/R)(∂A/∂φ) =
= (1/R)*A₀p·sin(ωt - pφ)
thus A₀ = B₀·R/p = 1 * 0.05 / 3 = 1/60

Due to periodicity of the problem, only half of the model is presented, and odd periodic boundary condition A₁ = -A₂ is applied on the cut. In fact, it would be enough to simulate just 60° sector of the model. In time domain, problem is simulated with automatic adaptive time step.

Results
Rotor eddy currents changing in time:

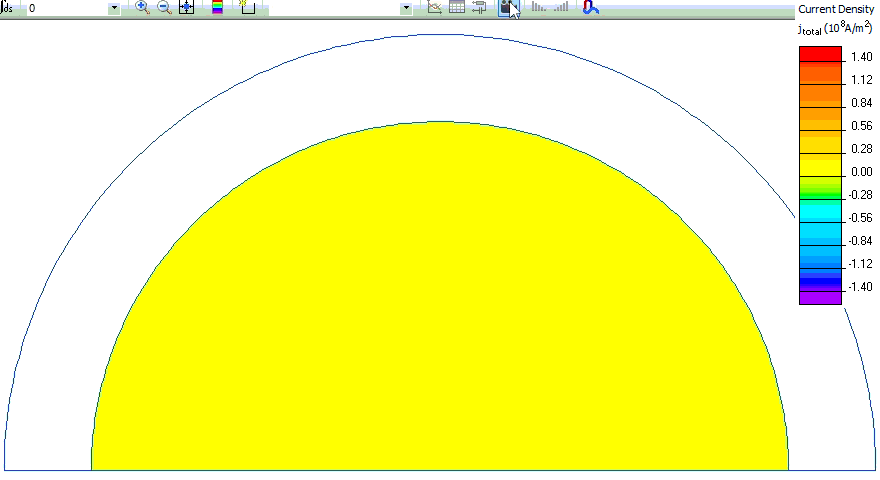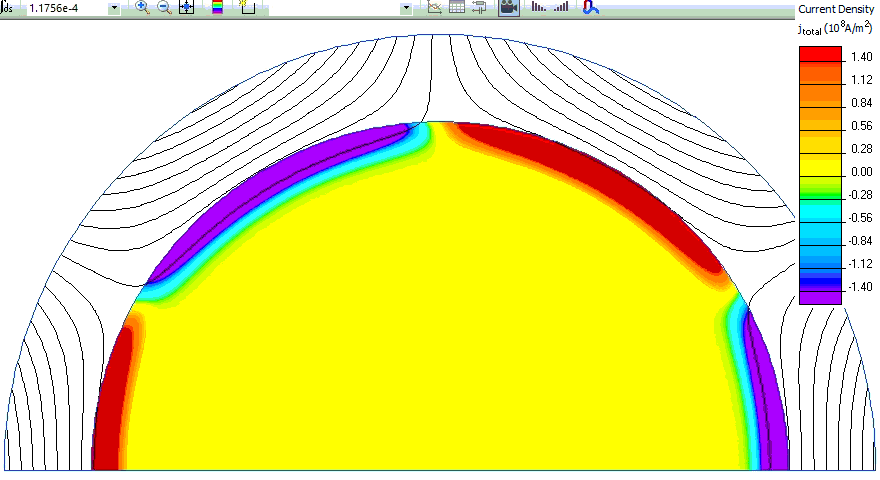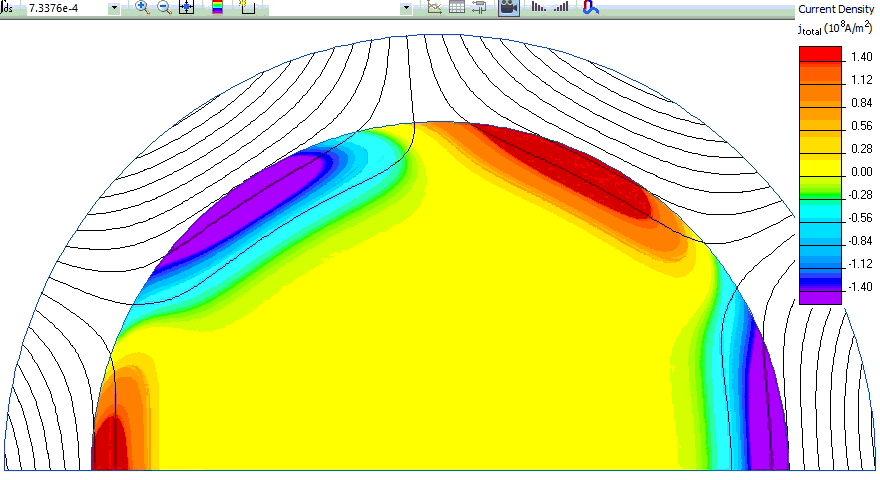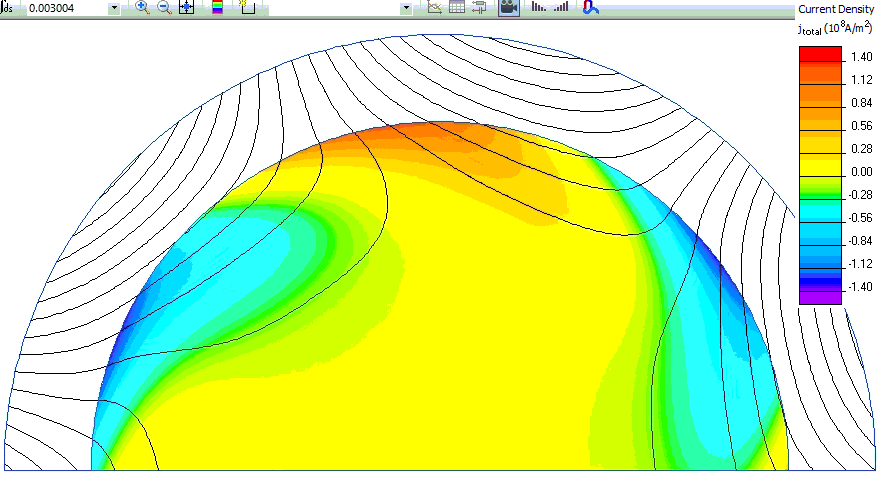
• Video: Conductive cylinder in rotating magnetic field. Watch on YouTube
  
• View simulation report in PDF.
• Download simulation files (files may be viewed using any QuickField Edition).