Industrial

Educational

Scientific

Engineering questions

Sample problems

Examples gallery

Step-by-step tutorials

Verification examples

Programming examples

Distributive examples

Success stories

Customers

Main >> Applications >> Sample problems

Shielded microstrip transmission line capacitance - QuickField simulation example

A shielded microstrip transmission line consists of a substrate, a microstrip, and a shield.

Engineering question

How to find microstrip transmission line capacitance?

Answer
Set up a plane-parallel QuickField Electrostatics problem for a microstrip transmission line and evaluate capacitance from computed field results.

More questions →

Typical applications
microstrip PCB traces, planar transmission lines, RF PCB layouts

Microstrip transmission line

Download

Simulation problem

Problem Type
Plane-parallel problem of electrostatics.

Geometry

The transmission line is directed along z-axis, its cross section is shown on the sketch. The rectangle ABCD is a section of the shield, the line EF represents a conductor strip.
Shielded microstrip transmission line capacitance A shielded microstrip transmission line consists of a substrate, a microstrip, and a shield. Strip Ground Air Substrate A B C D E F 10 mm 100 mm 100 mm 10 mm

Model depth Lz = 1 m.

Given
Relative permittivity of air ε = 1;
Relative permittivity of substrate ε = 10.

Task
Determine the capacitance of a microstrip transmission line.

Solution
There are several different approaches to calculate the capacitance of the line:

  1. Apply some distinct potential to the strip and calculate the charge that arises on the strip;
  2. Describe the strip as having constant but unknown potential and charge it with some distrinc value, then measure the potential that arises on the strip.

Results
Electric field strength distribution in a microstrip transmission line. Approach 1.
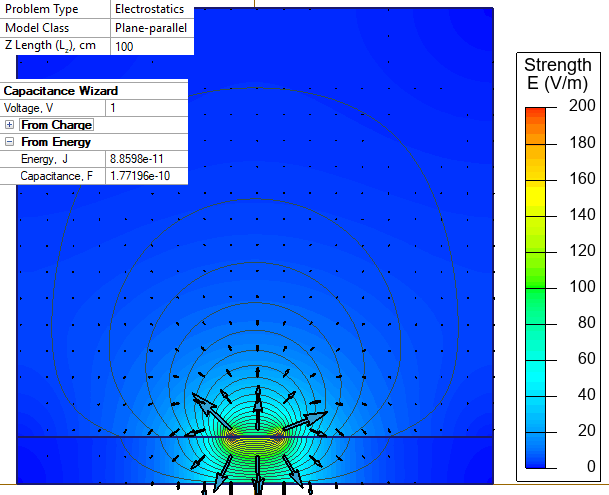
Shielded microstrip transmission line capacitance

Theoretical result [1] (model depth L = 1 m.) C = 178.074 pF.
Approach 1. C = q/U C = 178.36 pF
Approach 1. C = 2*W/U² C = 177.196 pF
Approach 2. C = q/U C = 178.31 pF)
Approach 2. C = 2*W/U² C = 177.191 pF

Reference
[1] Ostergaard, D. F. (1987). Adapting available finite element heat transfer programs to solve 2-D and 3-D electrostatic field problems. Journal of Electrostatics, 19(2), 151–164.

Video

Related examples