|
Main > Application > Sample problems
Charged particle trajectory in the uniform static electric field. Case: plane-parallel.
Problem Type:
Plane-parallel problem of electrostatics.
Geometry:
Distance between the plates d = 1 m.
Given:
Relative permittivity of vacuum ε = 1;
Positive potential U+ = 20 V.
Charge (electron) q = -1.602e-19 C
Mass (electron) m = 9.109e-31 kg
Initial velocity vx = vx = 500 000 m/s; vz = 0 m/s.
Emitter position (0; 0; 0) m.
Problem:
Calculate the particle trajectory neglecting relativistic effects.
Solution:
The analytical solution gives parabolic trajectory.
x(t) = vx*t [m],
y(t) = 0.5 * Fy / m * t2 [m],
z(t) = 0 [m],
where Fy = q*Ey - is the y-component of the Lorentz force,
t - is time.
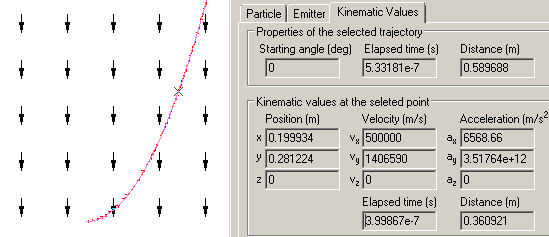
Particle trajectory may be calculated using the built-in function in QuickField Electrostatic postprocessor or by the free tool TrajectoryTracer.
Results:
Electric field strength Ex = 0 V/m, Ey = -20 V/m.
Lorentz force Fy = -1.602e-19 * -20 = 3.204e-18 N.
x(t) = 5e5*t m,
y(t) = 0.5*3.204e-18/9.109e-31 * t2 m,
z(t) = 0 m.
|
Particle coordinates (x; y; z) m |
time |
Theory |
QuickField |
TrajectoryTracer tool |
0 s |
(0; 0; 0) |
(0; 0; 0) |
(0; 0; 0) |
1e-7 s |
(0.050; 0.018; 0) |
(0.050; 0.018; 0) |
(0.050; 0.018; 0) |
2e-7 s |
(0.100; 0.070; 0) |
(0.100; 0.070; 0) |
(0.100; 0.070; 0) |
3e-7 s |
(0.150; 0.158; 0) |
(0.150; 0.158; 0) |
(0.150; 0.158; 0) |
4e-7 s |
(0.200; 0.281; 0) |
(0.200; 0.281; 0) |
(0.200; 0.281; 0) |
5e-7 s |
(0.250; 0.440; 0) |
(0.250; 0.440; 0) |
(0.250; 0.440; 0) |
 Download simulation files.
|
