Charged particle trajectory in the uniform static magnetic field. Case: plane-parallel.

QuickField simulation example

Problem Type
Plane-parallel problem of DC magnetics.

Geometry

Given
Relative permeability of vacuum μ = 1;
External field flux density B_x = -4 mT.
Charge (electron) q = -1.602e-19 C;
Mass (electron) m = 9.109e-31 kg;
Initial velocity v_x=v_y=5e6 m/s; v_z = 0 m/s.
Emitter position (0; 0; 0).

Task
Calculate charged particle trajectory in magnetic field neglecting relativistic effects.

Solution
The analytical solution gives spiral trajectory.
Radius in YZ-plane R_YZ = v_y / B_x * m/q [m].
Period T = 2π / B_x * m/q [s].
Lorentz force F_z = q*v_y*B_x [N].

To calculate the particle trajectory in QuickField free tool TrajectoryTracer is used.

Results

Analytical solution:
Radius in YZ-plane R_YZ = (5e6/0.004) * (9.109e-31/1.602e-19) = 0.00711 m.
Period T = (2*3.142/0.04) * (9.109e-31/1.602e-19) = 8.93e-9 s.
Lorentz force F_z = 1.602e-19 * 5e6 * 0.04 = 3.20e-15 N.

TrajectoryTracer tool:
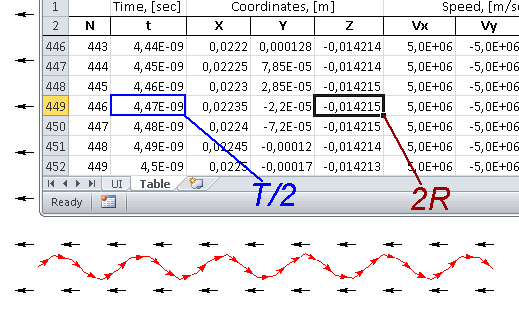
Radius in YZ-plane R_YZ = 0.14215/2 = 0.00711 m.
Period T = 4.47e-9*2 = 8.94e-9 s.
Lorentz force F_z = 3.20e-15 N.

• Video: Charged particle trajectory in the uniform static magnetic field. Case: plane-parallel. Watch on YouTube
  .
• View simulation report in PDF
• Download simulation files (files may be viewed using any QuickField Edition).