QuickField
A new approach to field modelling

Industrial

Educational

Scientific

Sample problems

Examples gallery

Step-by-step tutorials

Verification examples

Programming examples

Distributive examples

Success stories

Customers

Main >> Applications >> Sample problems >> Laminated iron core losses

Laminated core iron losses

QuickField simulation example

Problem Type
Plane-parallel problem of AC magnetics.

Geometry
Laminated core iron losses Calculate the core losses in the no-load mode of the single-phase transformer Core V1+ V1- V2- V2+ 20 mm 10 mm 10 mm 10 mm 50 mm 20 mm

Given

Winding1 number of turns 324.
Winding1 conductor cross-section 0.19 mm²
Winding1 average turn length 111 mm.
Winding1 no-load current 16.5 mA
AC frequency f = 400 Hz.
Core material density ρ = 7650 kg/m³
Core I permeability μ1 - nonlinear*
Core E permeability μ2 - nonlinear*

Task
Calculate the core losses in the no-load mode of transformer.

Solution
In no load mode the secondary winding is in open circuit state. There is current only in the primary winding. The primary winding is modelled as multi-turn winding - the average current density is specified.

Core is laminated, zero conductivity is specified. Core losses are calculated using Bertotti equation:
pv = kh·f·Bm² + kc·f²·Bm² + ke·(f·Bm)3/2
Coefficients kh, kc, ke are calculated as a result of the curve fitting using free utility Core loss coefficients calculator.

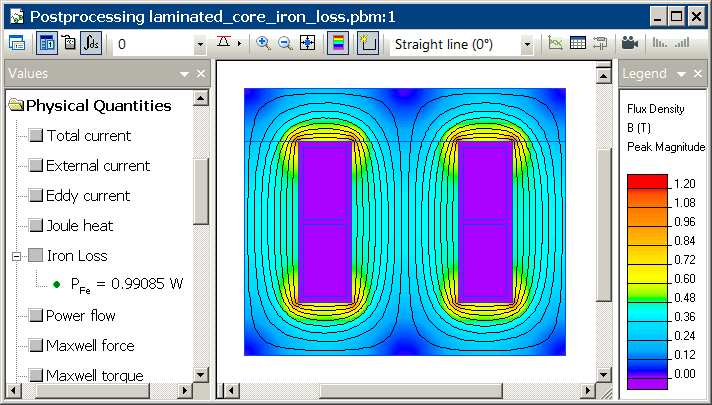
Results
Core E magnetic loss is 0.87 W.
Core I magnetic loss is 0.12 W.
Flux density distribution in the core:
laminated core magnetic loss

* Reference: Core loss and magnetization curves are provided by Arnold Magnetics.