Coulomb's law

QuickField simulation example

This example shows the calculation of the electrostatic force between two charged conductive spheres and result comparison with the classical Coulomb's law.

Problem Type
Axisymmetric problem of electrostatics.

Geometry

Given
Air relative permittivity ε = 1;
Sphere electric charge Q+ = |Q-| = 0.1 nC.

Task
Calculate the charged bodies attraction force and compare the value with analytical solution.

Solution
Charged conductive sphere in QuickField may be defined by specifying the equipotential surface boundary condition and applying the charge to one node on this surface. This charge will be distributed between all equipotential nodes.
If the distance between the spheres is much larger than sphere radius, they may be considered as point charges, and Coulomb's law may be applied. It states that the force between the point charges could be calculated as*
f = (1/4πε) * (|Q+|*|Q-|) / R²
*Wikipedia: Coulomb's law.

Result
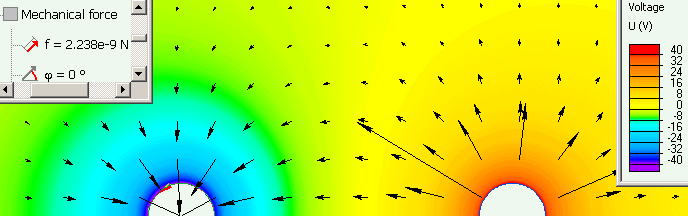
Force given by the Coulomb's law: f = 1 / (4*3.142*8.854e-12) * (1e-10 * 1e-10) / 0.02² = 2.247 nN.

Electric potential distribution simulated in QuickField is shown on the picture below. Coulomb's force calculated by QuickField is f = 2.238 nN.
A small difference between the numerical simulation and analytic results may be attributed to the fact that spheres have non zero radii and their interaction is not exactly as of point charges.

• Video: Coulomb's law. Watch on YouTube
  
• Download simulation files (files may be viewed using any QuickField Edition).