Faraday's law of electromagnetic induction
QuickField simulation example
This example demonstrates the appearance of a current in a closed coil when a permanent magnet is moved into the coil.
Task type:
An axisymmetric problem of transient magnetics.
Geometry
Given
The coil contains 200 turns of a 0.25 mm² wire.
Permanent magnet coercive force Hc = 500 kA/m.
Magnet motion speed v = -9 cm/s.
Task
Calculate the induced current in the coil as a function of time (permanent magnet position)
Solution
To simulate the motion of a magnet, the coercive force is represented by a formula of coordinates (x) and time (t).
Hc*impulse(x + v*(t-1.02)*step(t-1.02),0.08,0.1)
The impulse function describes the spatial pulse along the x axis in the range from 0.08 m to 0.10 m (the pulse spatial length 20 mm is equal to the axial length of the permanent magnet).
The pulse moves in space with a speed v.
Transient problem uses zero magnetic flux density distribution as the initial condition. Suddenly permanent magnet appears and causes the magnetic field distortion. It takes time for the disturbances caused by the appearance of the magnet to calm down. Therefore, we delay the motion start for a period of 1.02 s The delay is implemented by the step function.
You can study the function behavior in details using QuickField formula plotter online tool.
Result
Graph of current dependence and flux density distribution for specific moments of time.
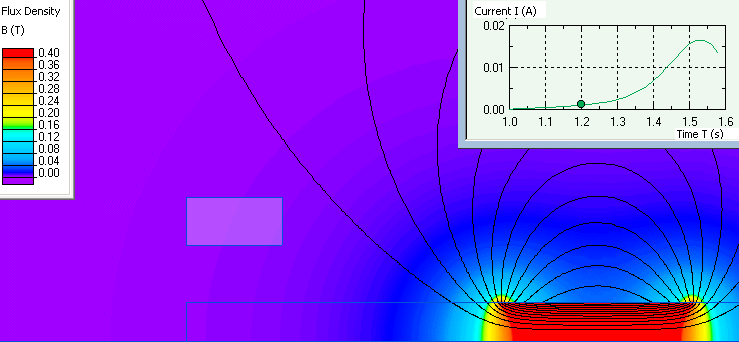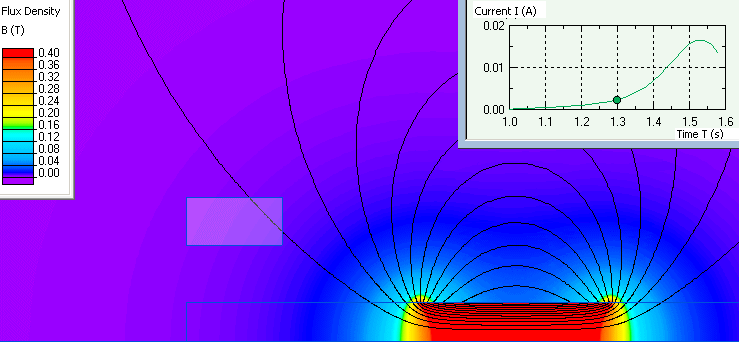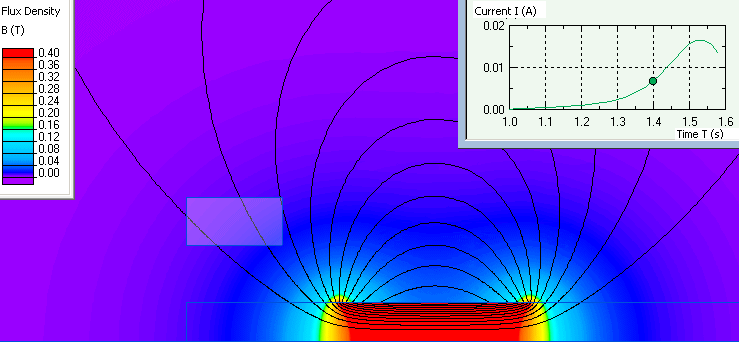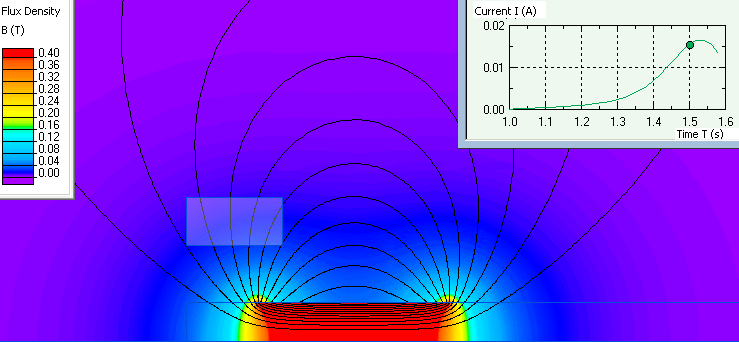
- Video: Faraday's law of electromagnetic induction. Watch on YouTube
- Download simulation files (files may be viewed using any QuickField Edition).
Reference: Wikipedia: Faraday's law of induction.