Problem Type Plane-parallel problem of DC conduction.
Geometry
Given Indium tin oxide film thickness t = 170 nm, sheet resistance Rs = 12.6 Ω/sq.
Electrode thickness d = 2 μm, copper electric conductivity σ = 56 MS/m.
Voltage V+ = 220 V.
Task Calculate the current and the Joule heat power.
Solution Film resistivity* ρ = Rs * t = 12.6 * 170e-9 = 2.142 μΩ*m. In QuickField DC conduction analysis we specify the electrical conductivity, that is reciprocal to the resistivity σ = 1 / ρ = 1/2.124e-6 = 467 kS/m.
Electrodes and film thickness are different. To be able to simulate this model in 2D we reduce the electrodes thickness to that of the film and proportionally increase the conductivity σ*d/t = 56 MS/m * 2μm/170nm = 659 MS/m.
Heat power distribution in the film is not uniform, so is the temperature. To get accurate results that take into account the heat redistribution inside the glass we should simulate a 3D heat-transfer problem.
Alternatively we can ignore the fact that the heat is redistributed in the glass and use this example to remap volume heating power Q to temperatures.
First we convert volume power to a surface power q[W/m²] = Q [W/m³] * t [m]
Then we can use the data from the table to get temperature values.
Glass temperature as a function of the heater power
q W/m²
Glass temperature
Inner side
Outer side
0
-5.56°C
-7.13°C
1000
29.5°C
22.08°C
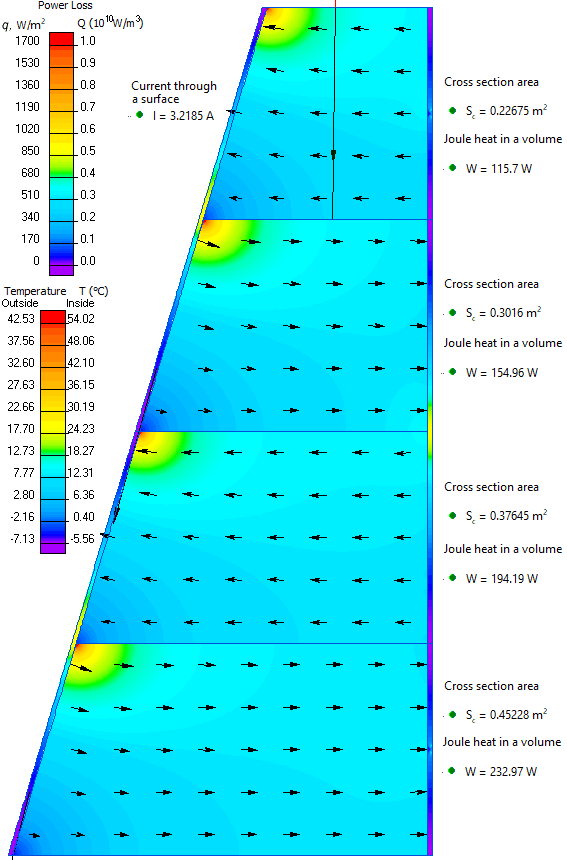
Result Electric current is I = 3.218 A. Total power is 220 V * 3.218 A = 708 W.
Power dissipated in the film
Section
Area, m²
Power, W
Power/Area, W/m²
#1 (top)
0.22675
115.7
510
#2
0.3016
154.96
514
#3
0.37645
194.19
516
#4 (bottom)
0.45228
232.97
515
Total
1.357
697.82
-
The difference (708 - 697.82) W is dissipated in the copper electrodes.
