Harmonic analysis of saw function
QuickField simulation example
This example demonstrates the accuracy of the harmonic browser (included in QuickField package)
Rectangular wave duct consists of two electrodes. The electrodes carry electric potential in a form of saw-function. Perform Fourier analysis of electric potential distribution.
Problem Type
Plane-parallel problem of electrostatics.
Geometry
Given
Relative permittivity of air ε = 1,
Boundary potentials - saw function.
Task
Perform the Fourier analysis of the voltage distribution curve. Use the harmonic browser to calculate amplitudes of the harmonics and compare results with analytical solution.
Solution
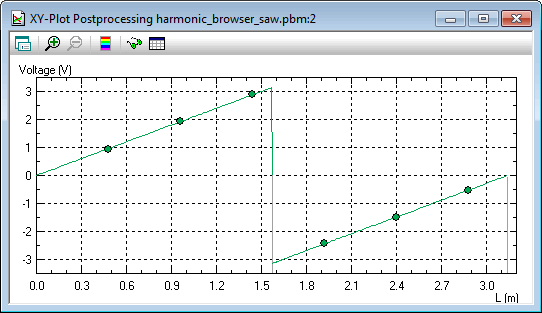
Voltage distribution along the X axis corresponds to the "saw" function.
U(0≤x<1.507) = 2·x
U(x=1.507) = 0
U(1.507<x≤3.142) = 2·x - 2·π
Fourier analysis of this "saw" function gives the following analytical solution:*
f(x) = 2 · ( sin(x) - sin(2x) / 2 + sin(3x) / 3 - ... + (-1)n+1·sin(nx) / n )
Results
Potential distribution along the bottom boundary
Harmonic browsers window
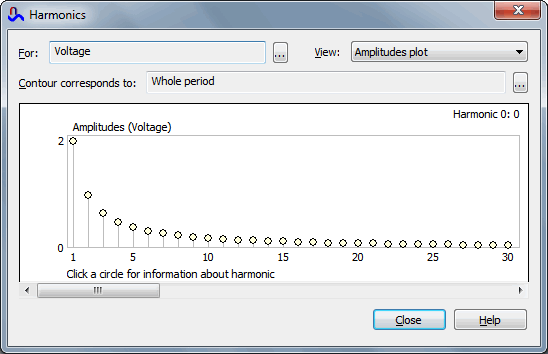
Harmonic browser allows calculation of the first hundred harmonics.
|
Harmonic |
Amplitude |
Error | |
|
QuickField |
Theory | ||
| 1 | 2 | 2 | - |
| 2 | 0.9999 | 1 | - |
| 3 | 0.6666 | 0.6666 | - |
| 4 | 0.4999 | 0.5 | - |
| 5 | 0.3999 | 0.4 | - |
| 10 | 0.1999 | 0.2 | 0.05% |
| 20 | 0.0998 | 0.1 | 0.2% |
| 50 | 0.0383 | 0.04 | 5% |
| 100 | 0.0168 | 0.02 | 15% |
*Mathematical Methods for Physicists. A Comprehensive Guide. 7th Edition. George Arfken, Hans Weber, Frank Harris, p 937-938. ISBN 978-0-12-384654-9.
- Video: Harmonic analysis of saw function
- View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).