Induction pump
QuickField simulation example
In the induction pump the alternating magnetic field induces eddy currents in the liquid metal. Interaction between the magnetic field and the currents generate the force which moves the metal through the pipe. The eddy currents value depends on the metal conductivity, which depends on temperature. Calculate the pump force and pressure as functions of temperature.
Problem Type
Axisymmetric problem of AC magnetics.
Geometry
Given
Winding current density j = 6 A/mm²
Frequency f = 50 Hz
Magnetic permeability of the steel core μ = 200;
Conductivity of the liquid metal σ - depends on temperature, as shown on the plot below;
Task
Calculate the pump force and pressure as functions of temperature.
Solution
Due to the axial symmetry only the upper half is presented in the model.
As the induced current rapidly fades outside the inductor it is possible to limit the model z-length by 400 mm.
Conductivity vs. temperature dependency was specified for the 'liquid metal' block.
The series of problems was solved for the temperature range 600-900°C. The mechanical force acting on the liquid metal was calculated at each step.
Pressure [Pa] = Force [N] / Cross-section area [m²]
Results
Eddy currents distribution in the liquid metal
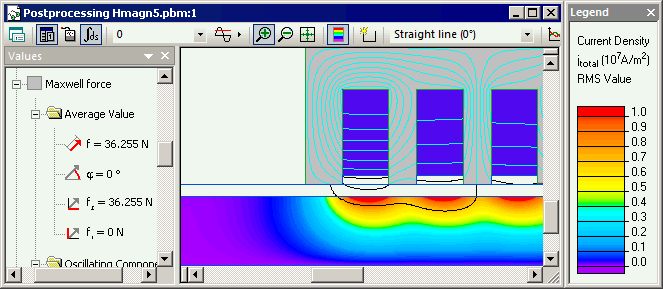
| Temperature, °C | Force, N | Pressure, kPa |
|---|---|---|
| 100 | 41 | 14.5 |
| 200 | 30 | 10.5 |
| 600 | 23 | 8.1 |
| 900 | 18 | 6.5 |
Reference: Inductive pump
- Video: Induction pump. Watch on YouTube
. - View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).