Joule-Lenz law
QuickField simulation example
This verification example compares the current and the Joule heat generated in conductor calculated by the Ohm's law and Joule's law, and calculated in QuickField using three formulations: DC conduction, AC conduction and Transient electric.
Geometry
Given
V = 0.1 V - voltage applied;
f = 50 Hz - frequency in time harmonics and transient magnetics problems;
g = 1 MS/m - conductivity of conductor material.
L = 0.4 m - conductor length.
A = 0.02*0.005 m² - conductor cross-section area.
Task
Calculate the current and Joule heat inside the conductor and compare with the value given by the Joule-Lenz law.
Solution
To maintain the same value of Joule heat across all formulations the voltage value is adjusted:
In the time harmonics problem peak amplitude value of voltage is set √2·V.
In the transient electric voltage is set via formula V(t) = √2·V · sin(2·180·50·t).
According to the Joule-Lenz law* the power of heating generated by an electrical current I:
W = R*I²,
where the conductor resistance is R = (1/g) * (L/A).
The electric current value could be calculated I = V / R [A],
Results
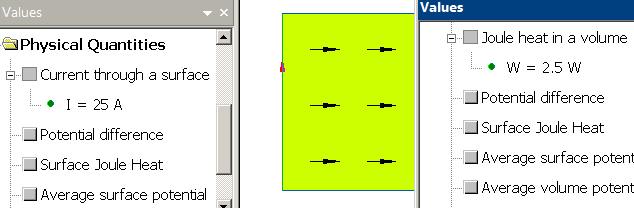
Conductor resistance R = (1/1e6) * (0.4/0.02*0.005) = 0.004 Ohm
Current: I = 0.1 / 0.004 = 25 A
Joule heat Q = 0.004 * 25 * 25 = 2.5 W.
DC conduction:
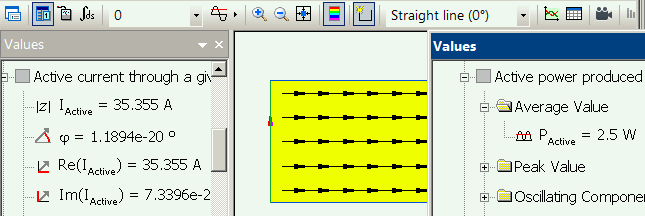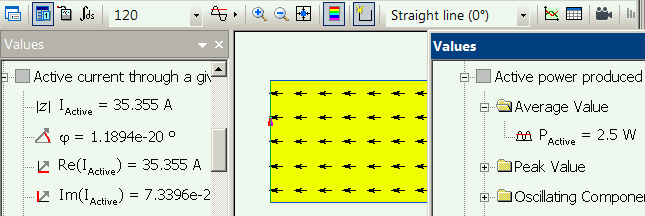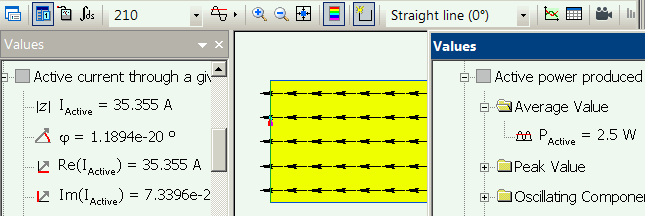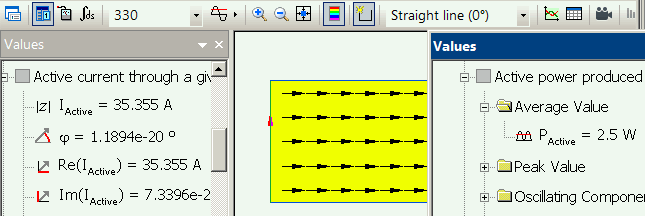
Time harmonics (peak current value is presented, RMS value is √2 times smaller, 35.355/1.4142 = 25 A):
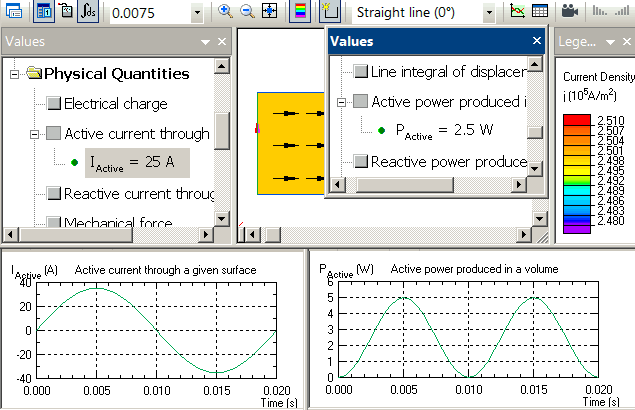
Transient electric:
| Time | Current | Joule heat |
| 0.01 s | 0 A | 0 W |
| 0.0125 s | 25 A | 2.5 W |
| 0.015 s | 35.355 A | 5 W |
| Heat power, W | |
|---|---|
| Joule-Lenz law | 2.5 |
| DC conduction | 2.5 |
| Time harmonics | 2.5 |
| Transient electric (time-average) | 2.5 |
- Video: Joule-Lenz law. Watch on YouTube
. - View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).