Pair of parallel wires capacitance

QuickField simulation example

Problem Type
Plane-parallel problem of electrostatics.

Geometry

a1 = 4 mm, a2 = 1 mm, b = 10 mm.

Given
Relative permittivity of air ε = 1,
Charge value q = 1 nC.

Task
Find the mutual capacitance between two parallel wires and compare its value with analytical solution*:
C/L_z = 4π·ε·ε₀ / 2·LN [ (b²-a1²-a2² + 2bc) / 2·a1·a2 ] [F/m],
where 2bc = √[b² - (a1+a2)²] · [b² - (a1-a2)²] [m²]

Solution
Wire's surfaces are marked as 'floating conductor', i.e. isolated conductors with unknown potential. At some point on each of wire's surface the charge q is applied. The charge is then redistributed along the conductor surface automatically.
QuickField calculates electric potential U distribution. The capacitance is calculated as C = q / ΔU.
In problem properties we set model depth to be L_z = 1 m.

Results
Analytical solution 2bc = √[0.01² - (0.004+0.001)²] · [0.01² - (0.004-0.001)²] = 8.261e-5 m².
C/L_z = 4·3.142·1·8.854e-12 / 2·LN [ (0.01²-0.004²-0.001² + 8.261e-5) / (2·0.004·0.001) ] = 18.36 pF/m.

The measured potential difference in QuickField is ΔU = 54.41 V.
The capacitance is C = 1 nC / 54.41 V = 18.38 pF per model depth L_z = 1 m.
Electric potential distribution around parallel wires calculated in QuickField:

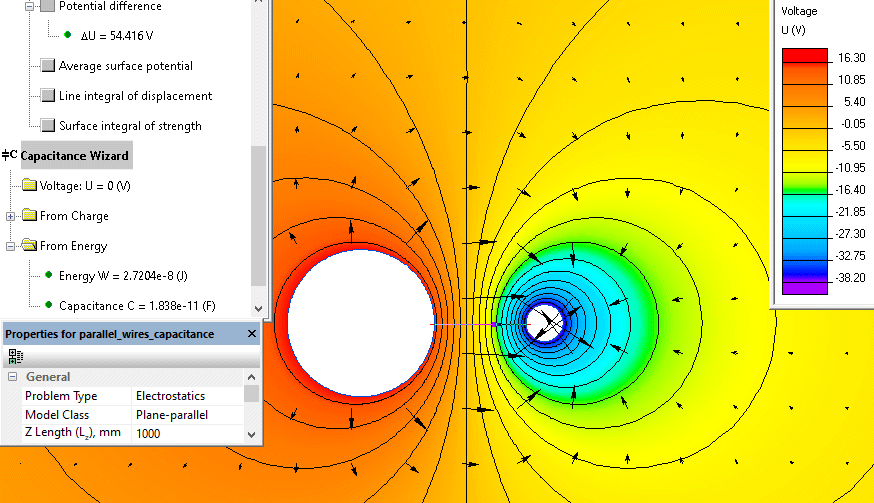
*Reference: Chester Snow Formulas for Computing Capacitance and Inductance, U.S. Government Printing Office, 1954

• Video: Pair of parallel wires capacitance
  
• Watch on YouTube.
• View simulation report in PDF
• Download simulation files (files may be viewed using any QuickField Edition).