Spherical capacitor

QuickField simulation example

Problem Type
Axisymmetric problem of electrostatics.

Geometry

R = 100 mm, R=50 mm.

Given
Relative permittivity of air ε = 1,
The charge q = 10^-9 C

Task
Find the capacitance of spherical capacitor and compare it with analytical solution:
C = 4π·ε·ε₀ · r·R / (R - r), [F]. *

Solution
Capacitor plate's surface is marked as 'floating conductor', i.e. isolated conductors with unknown potential. At some point on spheres' surface the charge is applied. The charge is then redistributed along the conductor surface automatically.

Results
Potential distribution inside of the spherical capacitor.

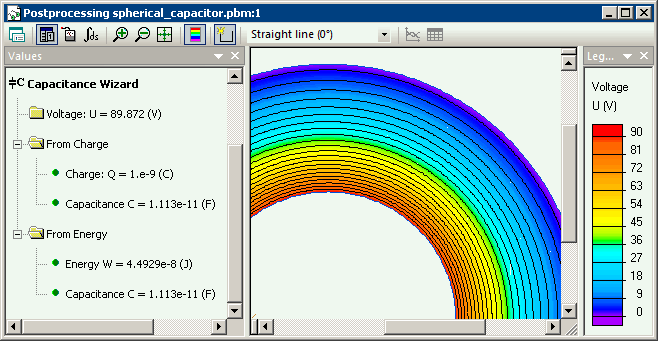
The capacitance can be calculated as C = q / (U2-U1).

The measured potential difference is U2-U1 = 89.87 V.
The capacitance is C = 10^-9/ 89.87 = 11.13·10^-12  F

Reference: Wikipedia, Capacitance.

• Video: Spherical capacitor 2D axisymmetric. Watch on YouTube
  

  Spherical capacitor 3D. Watch on YouTube.

• View simulation report in PDF
• Download simulation files (files may be viewed using any QuickField Edition).