Electromagnetic shielding - QuickField simulation example
Uniform external magnetic field is produced by the electric magnet. The shield with the measuring coil inside is placed between its poles. EMF in the coil is measured: in case of DC current in the coil - by ballistic galvanometer (in the moment of switching on), in case of AC current - by use of voltmeter.
Engineering question
How to find magnetic field reduction inside cylindrical shield?
Answer Set up an axisymmetric QuickField DC Magnetics problem for a cylindrical shield and evaluate magnetic field reduction from computed field results.
Problem Type Axisymmetric problem of DC magnetics.
Geometry The shield consists of two halves. The gap could be enlarged up to 2 mm by sheets of non-magnetic materials.
Given Electrical conductivity of copper 57 MS/m.
Electrical conductivity of steel 10 MS/m.
Relative magnetic permeability of steel μ=1000.
External magnetic field flux density B = 0.139 T (peak value for AC magnetic problem).
Task Find the level of magnetic field reduction inside the shield. Shields made of steel and copper of the same geometry are analyzed.
Solution Due to symmetry of the model the simulation domain is requced to a quater of a full model.
External magnetic field is specified by the boundary condition A=0.0695 Wb at the top boundary.
Results Current density in cylindrical and spherical shielding:
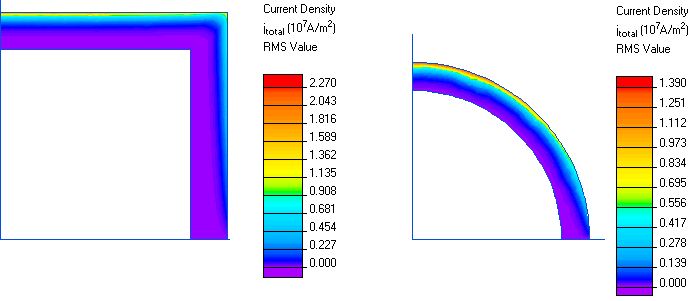
Shielding coefficient - relation of magnetic flux densities outside and inside the shield.
Time-harmonic magnetic field, f=50 Hz
Shield type
Flux density inside, mT
Problem file
Steel cylinder
0.013
lab4cFe.pbm
Steel sphere
0.082
lab4Fe.pbm
Steel sphere with gap
36
lab4Fe+.pbm
Steel cylinder with gap
40
lab4c_Fe+.pbm
Copper cylinder
69
lab4cCu.pbm
Copper cylinder with gap
71
lab4cCu+.pbm
Copper sphere
98
lab4Cu.pbm
Copper sphere with gap
100
lab4Cu+.pbm
DC magnetic field
Shield type
Flux density inside, mT
Problem file
Steel sphere
1.5
lab4_f.pbm
Steel cylinder
2.1
lab4c_f.pbm
Steel sphere with gap
39
lab4_f+.pbm
Steel cylinder with gap
45
lab4c_f+.pbm
Video
Electromagnetic shielding. Cylindrical shield. Watch on YouTube.
