QuickField
A new approach to field modelling

Industrial

Educational

Scientific

Sample problems

Examples gallery

Step-by-step tutorials

Verification examples

Programming examples

Distributive examples

Success stories

Customers

Main >> Applications >> Sample problems >> Axial flux motor back EMF

Axial flux motor back EMF

QuickField simulation example

In this example we simulate the axial flux motor in a no-load mode and measure its back EMF. As there is no current in the stator winding, we can simulate it in DC magnetics: a set of problems is simulated with different rotor positions. The flux linkage with the winding is calculated and then converted into the electromotive force.
Motor dimensions are taken from this paper [1]. In general case the study requires 3D magnetic analysis. We used the 2D inner rotor modeling approach [2] to convert the 3D model into a set of 2D models.

Problem Type
A plane-parallel problem of DC magnetics.

Geometry
Stator core height 65.5 mm, tooth height 17.2 mm,
Rotor core height 55.6 mm, permanent magnet height 6.9 mm.
Axial flux motor In this example we simulate the axial flux motor in no-load mode and measure its back EMF. As there is no current in the stator winding we can simulate it in DC magnetics S S S S N N N N Stator Rotor A1 A2 A1+ A1- A2- A2+ B1 B2 C1 C2 Ø150mm Ø150mm 55.6 65.5 r4 r3 r2 r1

Given
Rotor angular velocity 341.88 [1/s].
Permanent magnet coercive force Hc = 890 kA/m, remanence 1.175 T.

Task
Calculate the back EMF in the stator windings.

Solution
To avoid complicated 3D magnetic analysis we transform the geometry model into a number of 2D models. First, we make several circular slices, four in this case, with radii r1, r2, r3, r4. Each slice represents a dr portion of the motor.

Axial flux motor. Circular slice at r1
Axial flux motor Circular slice Cut Stator A1 A2 B2 B1 C2 C1 r1 Air gap Rotor

Then we made a cut in the slice and unfold it.
Axial flux motor. Unfolded circular slice at r1
Stator Air gap 2·π·r1 Rotor A1 A2 B1 B2 C1 C2

Then we fold the slice to make a circle. The rotor is kept inside and the stator is kept outside. This approach is called 2D inner rotor modeling approach [2].
Axial flux motor. Folding of the slice into a circle
Stator Rotor A1 A2 B1 B2 C1 C2

Now we have a slice converted to a topology of a conventional rotating machine. LabelMover parametric tool is used to automatically rotate the rotor by 1° and measure the flux linkage with stator windings. Then the flux linkage vs. angle dependency is converted into the induced voltage vs. time dependency: EMF = - d(Flux) d(t) = - d(Flux) d(angle) * d(angle) d(t) = - Δ Flux Δ angle * angular velocity

Result

Four slices converted to 2D rotational geometries of different size.

Axial flux motor 4 slices.
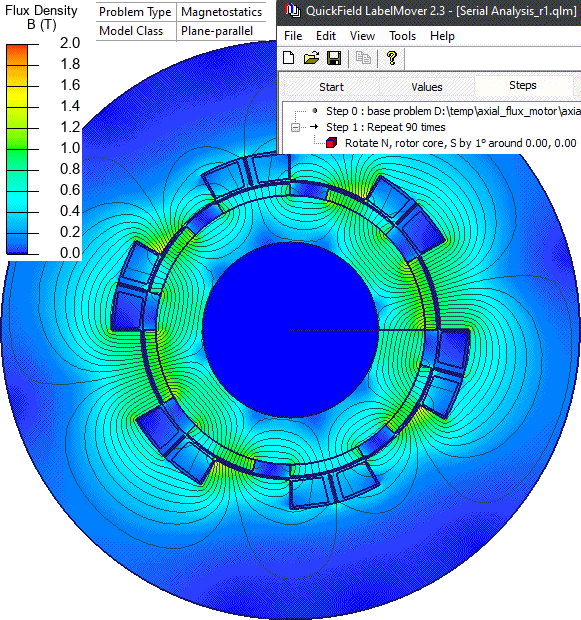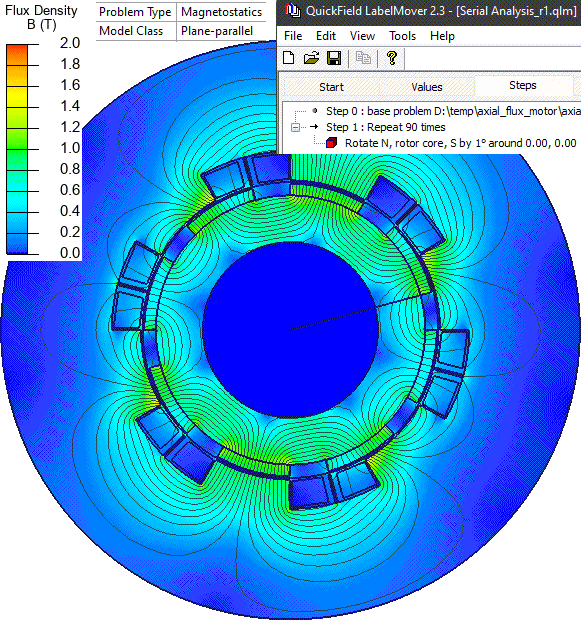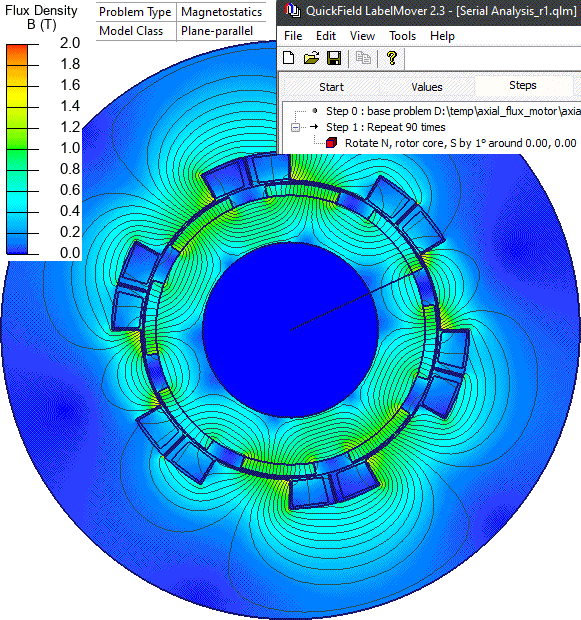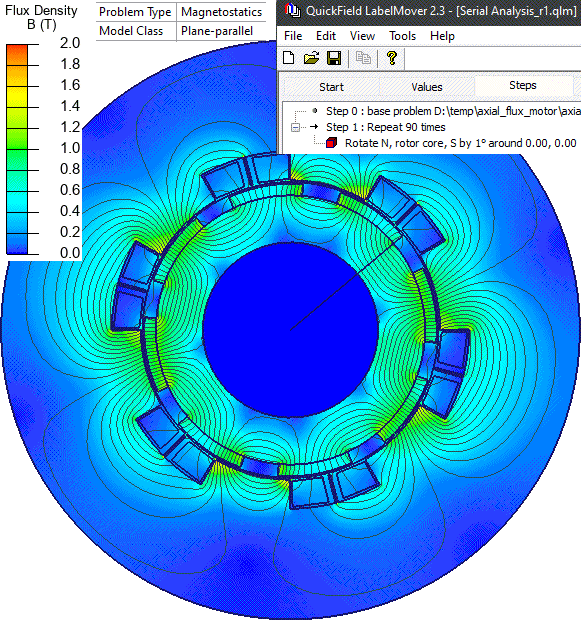
Axial flux motor. Variation of the magnetic field in the slice r1

Axial flux motor. Variation of the magnetic field

References:
[1] Nadia Chaker, Ibrahim Ben Salah, Souhir Tounsi, Rafik Neji Design of Axial-Flux Motor for Traction Application. J. Electromagnetic Analysis & Applications, 2009, 2: 73-83
[2] Mehmet Gulec, Metin Aydin. Implementation of different 2D finite element modelling approaches in axial flux permanent magnet disc machines. IET Electr. Power Appl. 2018, 12, 195–202.