Inductance of a pair of concentric cylinders
QuickField simulation example
A coaxial cable has an inner core of radius 1.0 mm and an outer sheath of internal radius of 4.0 mm. Determine the inductance of the cable per meter length.
Problem Type
Plane-parallel problem of AC magnetics.
Geometry
Inner radius a = 1 mm, outer radius b = 4 mm.
Given
Current I = 0.001 A;
Analytical solution*:
The total inductance per meter at low frequency is given by L = μ/2π · (1/4 + ln(b/a)) H/m
L = 4π·10-7 / 2π · (1/4 + ln(4)) = 3.27259·10-7 H/m
QuickField simulation results:
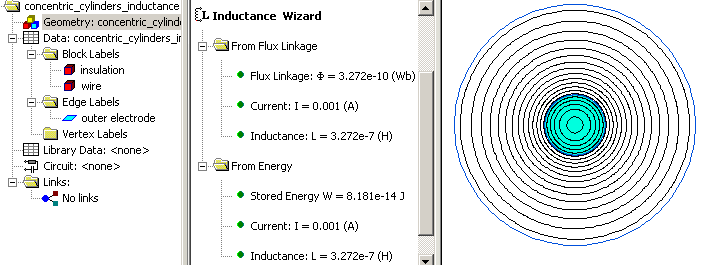
Note: QuickField calculates the total current and the total flux. To get RMS we should divide the corresponding amplitude value by root 2:
L = Flux / I = 3.272·10-10/1.4142 / 0.001/1.4142 = 3.272·10-7 H/m
L = 2·W / I² = 2·8.181·10-14 / (0.001/1.4142)² = 3.272·10-7 H/m
| Mesh size | QuickField | Discrepancy with analytical solution* | |
|---|---|---|---|
| L = Flux / I | L = 2·W / I² | ||
| 251 (QuickField Student Edition) | 3.23·10-7 H/m | 3.22·10-7 H/m | 1% / 1.55% |
| 1301 (automatic refinement in Professional Edition) | 3.267·10-7 H/m | 3.239·10-7 H/m | 0.17% / 1.03% |
| 4003 (automatic refinement 2) | 3.27·10-7 H/m | 3.263·10-7 H/m | 0.08% / 0.26% |
| 8814 (automatic refinement 3) | 3.271·10-7 H/m | 3.268·10-7 H/m | 0.05% / 0.14% |
| 26474 (automatic refinement 5) | 3.272·10-7 H/m | 3.271·10-7 H/m | 0.02% / 0.05% |
| 78585 (automatic refinement 10) | 3.272·10-7 H/m | 3.272·10-7 H/m | 0.02% / 0.02% |
*References: John Bird, "Electrical circuit theory and technology", p.520. ISBN-13: 978 0 7506 8139 1.
- Video: Inductance of a pair of concentric cylinders. Watch on YouTube
- View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).