|
Main >>
Applications >>
Sample problems >>
Capacitance matrix of two conductors transmission line
Two conductors transmission line
This is an example of the two conductors transmission line simulation, performed with QuickField software.
Problem type:
Plane-parallel problem of electrostatics.
Geometry:
The problem's region is bounded by ground from the bottom side and extended to infinity on other three sides.
Model depth l = 1 m.
Given:
Relative permittivity of air ε= 1;
Relative permittivity of dielectric ε= 2.
Problem:
Determine self and mutual capacitance of conductors.
Solution:
To avoid the influence of outer boundaries, we'll define the region as a rectangle large enough to neglect side effects. To calculate the capacitance matrix we set the voltage U = 1 V on one conductor and U = 0 on another one.
Self capacitance: C11 = C22 = Q1 / U1 ,
Mutual capacitance: C12 = C21 = Q2 / U1 ,
where charge Q1 and Q2 are evaluated on rectangular contours around conductor 1 and 2 away from their edges. We chose the contours for the C11 and C12 calculation to be rectangles [-6<x<0], [0<y<4] and [0 <x<6], [0<y<4] respectively.
Results:
Potential distribution in two conductors transmission line:
|
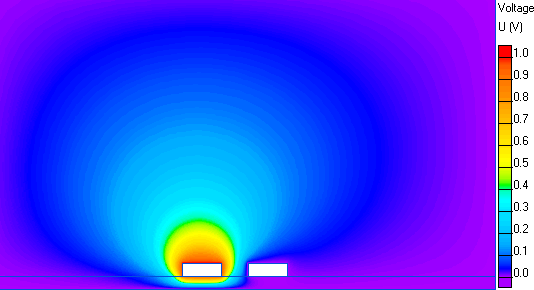
C11, F |
C12, F |
Reference* |
9.23·10-11 |
-8.50·10-12 |
QuickField |
9.43·10-11 |
-8.57·10-12 |
* Reference: A. Khebir, A. B. Kouki, and R. Mittra, An Absorbing Boundary Condition for Quasi-TEM Analysis of Microwave Transmission Lines via the Finite Element Method, Journal of Electromagnetic Waves and Applications, 1990.
 View simulation report in PDF.
 Download simulation files (files may be viewed using any QuickField Edition).
|
