Capacitance matrix calculation
Capacitance matrix provides the quantitative estimation of the mutual affect of the conductors in the electrostatic system. In practical engineering the field distribution in the system of conductors is replaced by the equivalent electric circuit consisting of capacitors.
Cable entries

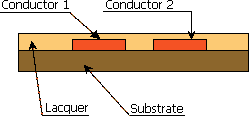
PCB conductors
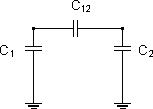
Equivalent schema
In the system consisting of several charged electrodes the potential of every electrode depends upon all the electrode charges. If the media properties are independent from the field (this condition is always supposed in the Electrostatic QuickField problems) this function may be presented as a linear equation:
U1 = a11 * q1 + a12 * q2 + ... + a1n * qn
U2 = a21 * q1 + a22 * q2 + ... + a2n * qn
......
Un = an1 * q1 + an2 * q2 + ... + ann * qn,
where
Uk - k-electrode potential,
qk - k-electrode charge,
aij - self and mutual potential coefficients.
Quite often the inverse problem-calculation of charges basing on the known potentials distribution arises. Resolving the system of equations (1) for charges (q1, q2, ... qn) yields to:
q1 = b11 * U1 + b12 * U2 + ... + b1n * Un
q2 = b21 * U1 + b22 * U2 + ... + b2n * Un
......
qn = bn1 * U1 + bn2 * U2 + ... + bnn * Un
In this system coefficients bij have dimensions of capacitance. They are usually called electrostatic induction coefficients or partial capacitances relative to ground. Coefficients bij may be positive or negative.
It is often required in practice to replace the conductors system by their equivalent schema, where each pair of conductors is presented by the capacitors with specially fitted capacitances. This form corresponds to the system of equations where the conductor charges are expressed through the potential differences between the conductor and other conductors, including earth:
q1 = c11 * (U1 - 0) + c12 * (U1 - U2) + ... + c1n * (U1 - Un)
q2 = c21 * (U2 - U1) + c22 * (U2 - 0) + ... + c2n * (U2 - Un)
......
qn = cn1 * (Un - U1) + cn2 * (Un - U2) + ... + cnn * (Un - 0)
Coefficients cij are called partial capacitances.
All three matrices are symmetrical, i.e cij = cji.
QuickField's capacitance matrix calculation add-in was designed to automate the frequent task of the grounded (b) and lumped (c) capacitance matrices calculation.

- You can find more information in User manual or QuickField help system.
- Video:
- Transmission line attenuation constant simulation example.