Planar film heater
QuickField simulation example
Electric current is passing through the contact electrode to the thin film heater.
Problem Type
Plane-parallel problem of DC Conduction and Heat Transfer.
Geometry
Model thickness Lz = 1 m.
Given
Indium tin oxide film thickness t = 170 nm, sheer resistance Rs = 12.6 Ohm/sq.
Electrical conductivity of copper 56 MS/m.
Electric current I = 5 A.
Thermal conductivity of glass 1 W/m*K.
Inside air temperature +20°C, surface resistance** 0.13 K·m²/W.
Outside air temperature -15°C, surface resistance** 0.04 K·m²/W.
Task
Calculate the heater power and the glass temperature.
Solution
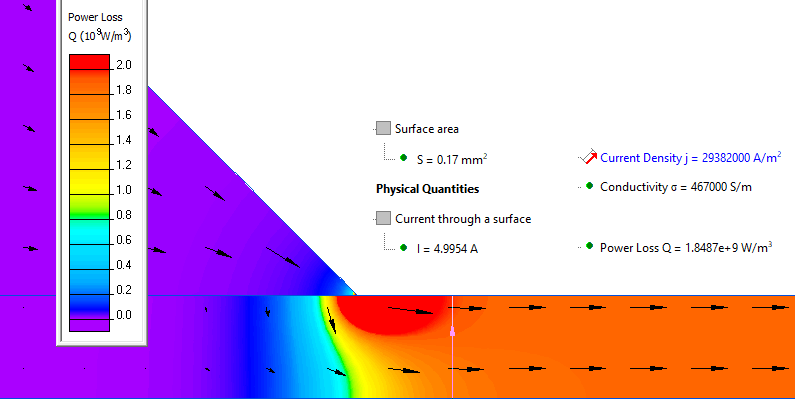
First we simulate DC conduction problem and calculate the heat power.
Film resistivity* ρ = Rs * t = 12.6 * 170e-9 = 2.142 μΩ*m. In QuickField DC conduction analysis we specify the electrical conductivity, that is reciprocal to the resistivity:
σ = 1 / ρ = 1/2.124e-6 = 467 kS/m.
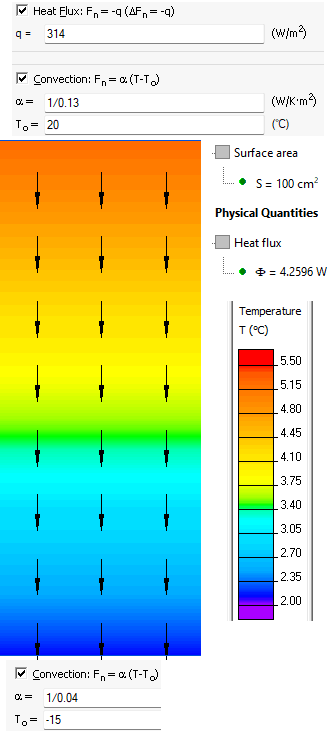
Joule heat is produced in a very thin film. Film thickness t is much less than that of a glass. We simplify the model for heat transfer analysis and replace the film with the edge with the known heat flux boundary condition:
Heat power [W/m²] = Volume power [W/m³] * t.
The convection coefficient value is reciprocal to the surface resistance value:
αinside = 1/0.13 W/(K·m²),
αoutside = 1/0.04 W/(K·m²).
Result
Film heater power is 1.848e9 W/m³ * 170nm = 314 W/m².
Glass temperature is calculated using simplified model with the film replaced by the boundary condition.
References:
* Wikipedia, Sheet resistance.
** ISO 10077-2:2012 Thermal performance of windows, doors and shutters.
- Video: Planar film heater. Watch on YouTube
- Download simulation files (files may be viewed using any QuickField Edition).