Gear wheel shrink fitting
QuickField simulation example
Simulation example of the gear wheel shrink fitting. The gear wheel was heated so that its internal diameter became slightly larger than the diameter of the shaft. After mounting the gear wheel is cooled down and decreased in size.
Problem type:
Plane-parallel problem of stress analysis.
Geometry
All dimensions are in millimeters.
Gear thickness H = 20 mm.
Given
Gear and shaft material - steel;
Young's moduli E = 2.11*1011 N/m²;
Poisson's rations ν = 0.26;
Coefficient of thermal expansions α = 1.2*105 1/K.
Overheating temperature T = 135 °C.
Task
Calculate the normal pressure.
Solution
The gear in the model is initially in a heated condition (already fitted to the shaft). In the properties of the gear wheel negative temperature is specified. Temperature value indicates how much the wheel has cooled. Thus, a reduction in the wheel size after fitting is simulated.
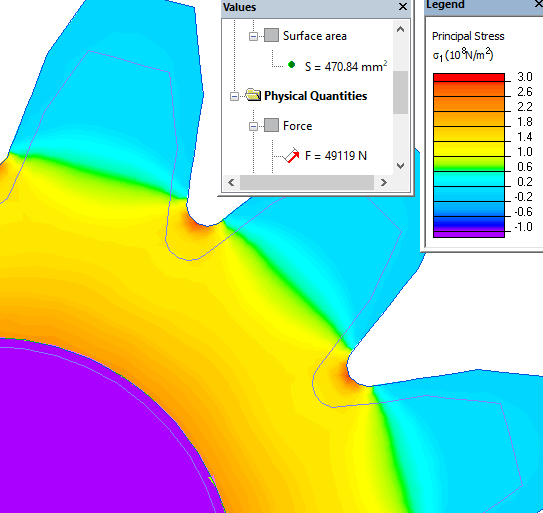
Using the integration contour, QuickField can calculate the force acting on the surface. If you draw a contour on the surface of the shaft, then the vector sum of the radial forces will be zero. To calculate the radial force we draw a contour over the surface of the shaft, using only a quarter of a circle.
Dividing the force value by the surface area, we get the normal pressure.
Results
Radial force acting on a quarter of a circle fr = 49 kN.
Normal pressure P = fr/S = 49*10³/470*10-6 = 104 MPa.
Mechanical stress distribution in the gear wheel:
- Download simulation files (files may be viewed using any QuickField Edition).