Cylinder with temperature dependent conductivity

QuickField simulation example

A very long cylinder (infinite length) is maintained at temperature T₁ along its internal surface and T₂ along its external surface. The thermal conductivity of the cylinder varies with temperature.

Problem Type
Axisymmetric problem of heat transfer.

Geometry
R1 = 5 mm, R2 = 10 mm;

Given
T₁ = 100 °C, T₂ = 0 °C;
Thermal conductivity λ(T) = 50 + 0.5·T.

Task
Determine the temperature distribution in the cylinder and compare with analytical solution*.

Solution
The axial length of the model is arbitrarily chosen to be 1 mm.

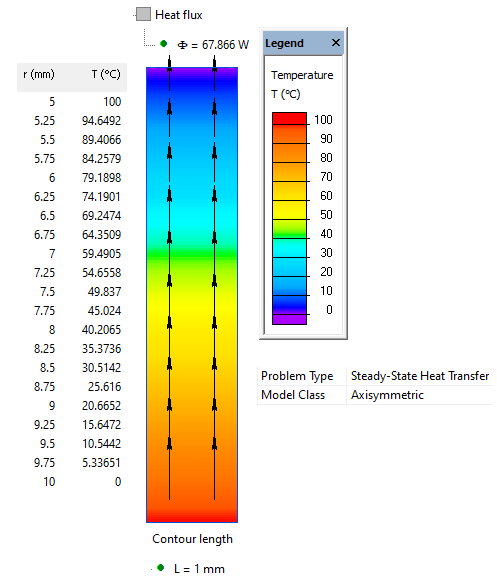
Results
Temperature distribution in a long cylinder:

Reference
* A Heat Transfer Textbook, 5th ed. John H. Lienhard IV, University of Houston John H. Lienhard V, Massachusetts Institute of Technology. Example 2.4. Radial Heat Conduction in a Tube.

• Video: Cylinder with temperature dependent conductivity
  
• View simulation report in PDF
• Download simulation files (files may be viewed using any QuickField Edition).