Multilayer coated pipe
QuickField simulation example
A very long cylindrical coated pipe (infinite length) is maintained at temperature Tinner along its internal surface and Touter along its external surface.
Problem Type
Plane and axisymmetric problems of heat transfer.
Geometry
Thin layer of 3 mm coating is placed between steel pipe and insulation.
Given
Tinner = 85°C, Touter = 4°C;
Thermal conductivity of steel λ=40 W/K-m,
Thermal conductivity of coating λ=0.4 W/K-m,
Thermal conductivity of insulation λ=0.15 W/K-m.
Task
Derive heat flux at the internal diameter and calculate the overall heat transfer coefficient (OHTC) of the system.
Solution
The OHTC of 3-layered pipe can be calculated as (*)
λtotal = 2πL / [ 1/λ1·ln(r2/r1) + 1/λ2·ln(r3/r2) + 1/λ3·ln(r4/r3)],
where L is the length of the tube.
For very long pipe the heat transfer in axial direction may be neglected, thus the temperature distribution in any cross section will be the same. In this case the plane-parallel can be solved. In plane-parallel problems all integral values are calculated per 1 meter of depth.
The axial length of the axisymmetric model does not affect to results, and was set to some small value (0.05 m) to reduce the mesh size. To convert heat flux (and other integral values) calculated in axisymmetric problem to flux calculated in plane-parallel problem the former should be multiplied by 20.
Results
Temperature distribution in multilayer coated pipe:
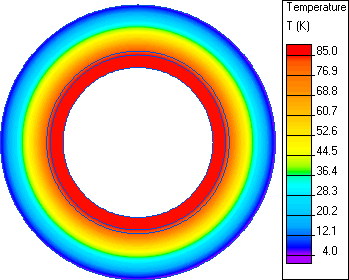
| QuickField | Reference* | ||
| plane | axisymmetric | ||
| Heat Flux, W | 178.2 | 8.89·20 = 177.8 | - |
|---|---|---|---|
| Temperature difference, K | 81 | 81 | 81 |
OHTC, W/K-m | 2.200 | 2.195 | 2.211 |
* Reference: H.Y. Wong Heat transfer for Engineers, Table 2.2 with the heat transfer coefficient set at infinity.
- Video: Multilayer coated pipe
- View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).