Equilibrium temperature

QuickField simulation example

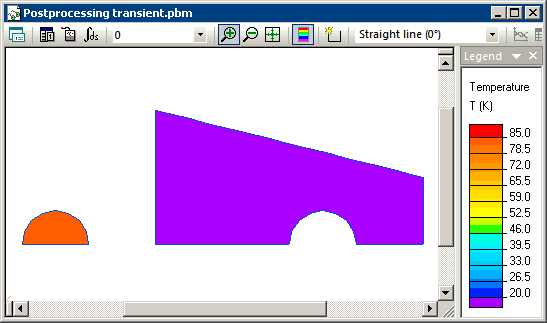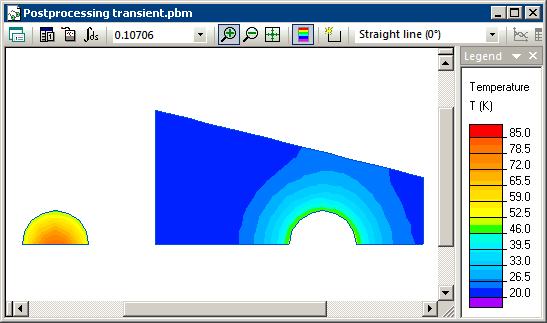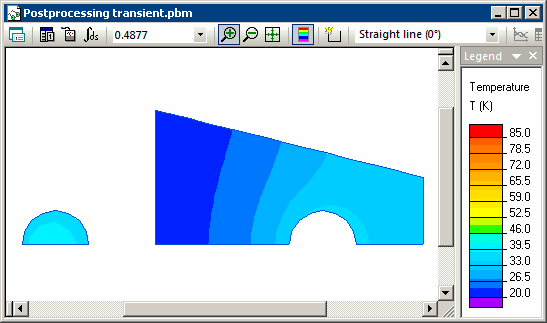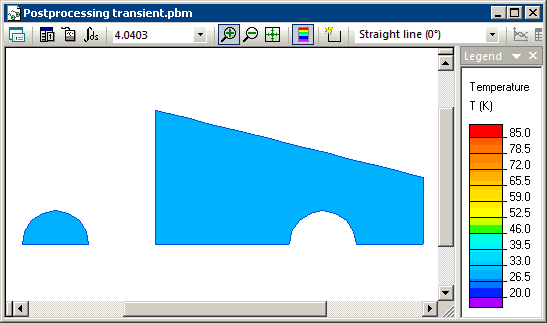
Hot steel sphere is submerged into a bucket with cold water. The steel sphere initial temperature is +85°C and the water initial temperature is +20°C. We The heat exchange with the surrounding media is ignored. We need to calculate the final equilibrium temperature of this system. This problem can be simulated with the QuickField transient heat transfer module.

Problem Type
Axisymmetric problem of transient heat transfer.

Geometry
Steel sphere volume V_steel = 65.4·cm³, water volume V_water = 3600 cm³.

Given
T_steel= 85°C, T_water=20°C;
Volume density of steel ρ_steel = 7800 kg/m³,
Volume density of water ρ_water = 1000 kg/m³,
Specific heat of steel C_steel = 460 J/kg·K,
Specific heat of water C_water = 4200 J/kg·K.

Task
Calculate the equilibrium temperature.

Solution
Initial non-uniformal temperature distribution is set by a special coupled static heat transfer problem. But taking into account that coupled problems should be based on the same geometry, we we have to separate water and steel in order to prevent heat exchange between them at the initial stage. That's why we set up the model with two separate regions.
Transient heat transfer simulation starts when steel and water are brought into contact and we model this using the periodic boundary condition (T1=T2) at their contact surfaces. Simulation shows that the temperatures of steel and water converge with time, and reach equilibrium level of 20.93 degrees at the end of the transient process.

For accuracy verification we use the analytical calculation. According to the 1^st law of thermodynamics, the energy of the isolated system is preserved [1]:
(CρV)_water·(T_water - T) + (CρV)_steel·(T_steel - T) = 0, where
T is the equilibrium temperature.

Results
Analytical solution
(CρV)_water = 4200·1000·3600·10^-6 = 15120 [J/K]
(CρV)_steel = 460·7800·65.4·10^-6 = 235 [J/K]
15120·(20 - T) + 235·(85 - T) = 0
T = 20.99°C

Temperature distribution calculated in QuickField (animation):

Reference:
[1] R.K. Rajput, A textbook of Engineering Thermodynamics. Third edition, SI units version. Publisher: Laxmi Publications pvt Ltd. February 10, 2011.

• Video: Equilibrium temperature. Watch on Youtube
  
• Download simulation files (files may be viewed using any QuickField Edition).