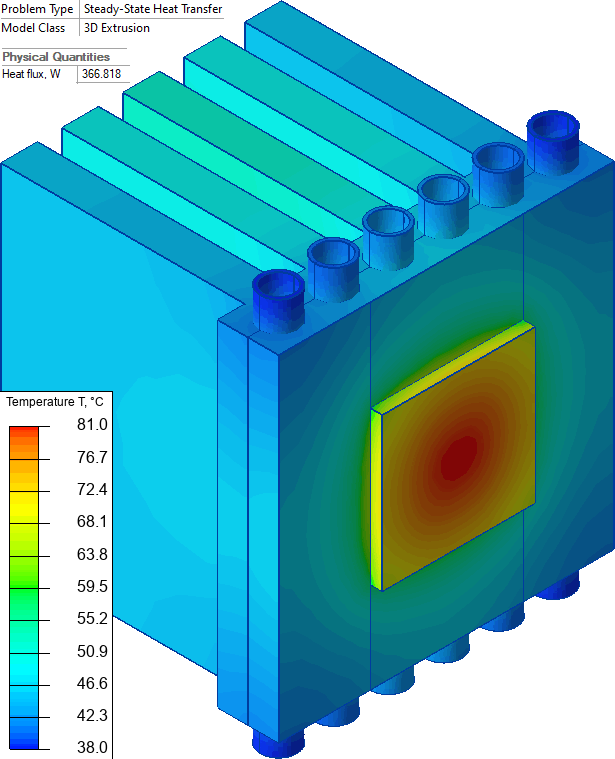
Heat sink
QuickField simulation example
Chip radiator heat sink is cooled by the air and the water.
Problem Type
3D problem of heat transfer.
Geometry
All dimensions are in millimeters.
Given
Thermal conductivity of aluminum 237 W/K-m, thermal conductivity of copper 380 W/K-m.
Air convection coefficient α = 10 W/(K·m²), ambient air temperature T0 = +20 °C.
Water convection coefficient* 2500 W/(K·m²), inlet water temperature +20 °C.
Heat flux q = 70 W/cm².
Task
Calculate the radiator temperature and the outlet water temperature.
Solution
As a first approximation we consider the water temperature to be constant along the heating channel. In fact the water heats up in the channels. The temperature rise can be calculated analytically** as ΔT = Heat flux * time / ( Water volume * density * heat capacity ), where time = channel length * velocity, and volume = channel length * cross-section area.
Water velocity* is 0.1 m/s, density 1000 kg/m³, heat capacity 4184 J/kg*°C.
Results
Heat flux that goes into the water is 366 W per 6 channels. The water temperature rise is ΔT = (366/6) * 0.1 / (19.6349e-6 * 1000 * 4184) = 0.074 °C. Our assumption that the water temperature is practically constant was correct.
References:
* General idea of the example, water convection coefficients and model dimensions are taken from the paper by Hassan Waqas, Shan Ali Khan, Umar Farooq, Taseer Muhammad, Ahmad Alshehri & Sumeira Yasmin. Thermal transport analysis of six circular microchannel heat sink using nanofluid. Scientific Reports volume 12, Article number: 8035 (2022).
** Wikipedia Specific heat capacity
- Download simulation files (files may be viewed using any QuickField Edition).