Symmetric double line of conductors

QuickField simulation example

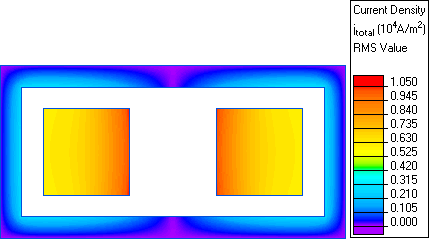
This is an example of the symmetric double line of conductors simulation, performed with QuickField software. Two copper square cross-section conductors with equal but opposite currents are contained inside rectangular ferromagnetic coating.

Problem Type
Plane-parallel problem of AC magnetics.

Geometry

Given
Magnetic permeability of air μ = 1;
Magnetic permeability of copper μ = 1;
Conductivity of copper σ = 56 MS/m;
Magnetic permeability of coating μ = 100;
Conductivity of coating σ = 10 MS/m;
Current in the conductors I = 1 A;
Frequency f = 100 Hz.

Task
Determine current distribution within the conductors and the coating, complex impedance of the line, and power losses in the coating.

Solution
We assume that the flux is contained within the coating, so we can put a Dirichlet boundary condition on the outer surface of the coating.

The complex impedance per unit length of the line can be obtained from the equation

Z = ΔV / I,
where ΔV = V₁ - V₂

V₁, V₂ are voltage drops per unit length in each conductor. To obtain a voltage drop, switch to Local Values mode in postprocessing window, and then pick an arbitrary point within a conductor.

To obtain power losses in the coating:

1. In the postprocessing mode, choose Pick Elements and pick the coating block to create the contour.
2. Choose Integral Values and select Joule heat from the list of integral quantities and choose Calculate.

Results
The impedance of the line Z = 0.000484 + i 0.000736 Ohm/m.
The power losses in the coating of the double line P = 0.0000427 W/m.

Current density in symmetric double line of conductors:

• View simulation report in PDF
• Download simulation files (files may be viewed using any QuickField Edition).