QuickField
A new approach to field modelling

Industrial

Educational

Scientific

Sample problems

Examples gallery

Step-by-step tutorials

Verification examples

Programming examples

Distributive examples

Success stories

Customers

Main >> Applications >> Sample problems >> Microstrip self impedance

Microstrip self impedance Z0

QuickField simulation example

This is an example of the microstrip line simulation, performed with QuickField software.

Problem Type
Plane-parallel problem of electrostatics and AC magnetics.

Geometry
Microstrip self impedance To calculate the impedance we should find the self capacitance and the self inductance Dielectric (ε=4.3) Copper 200 μm 420 μm 35

Given
Relative permittivity of air ε = 1;
Relative permittivity of dielectric ε = 4.3.
Frequency f = 500 MHz.
Line length Lz = 5 inches

Task
Determine the self impedance of the microstrip transmission line.

Solution
To calculate the impedance we should find the capacitance C0 and the inductance L0.
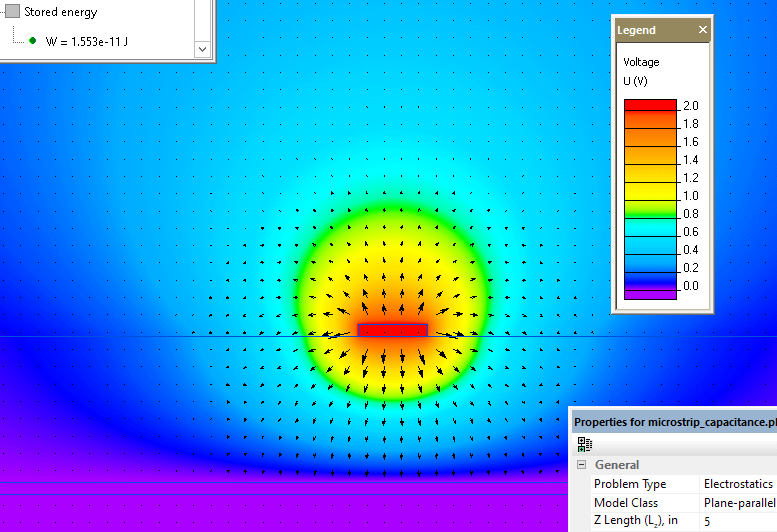
Capacitance is calculated in the electric problem. Positive potential is assigned to the conductor, zero potential is assigned to the ground plane. QuickField calculates the total stored electric field energy.
C0 = 2*Energy / ( Potential difference ) ²

Inductance is calculated in the AC magnetic problem. AC current In the conductor flows in one direction. The return current flows in the ground plane. QuickField calculates the total stored magnetic field energy.
L0 = 2*Energy / |Current| ²

Result
C0 = 2*1.553e-11 / 2² = 7.8 pF (per 5" of line length)
L0 = 2*3.35e-20 / (1e-6)² = 67 nH (per 5" of line length)
Impedance Z0 = √L0/C0 = 92.7 Ohm.

Voltage distribution in the microstrip line.
microstrip line self capacitance

Current density distribution in the microstrip line.
microstrip line self inductance