Industrial

Educational

Scientific

Engineering questions

Sample problems

Examples gallery

Step-by-step tutorials

Verification examples

Programming examples

Distributive examples

Success stories

Customers

Main >> Applications >> Sample problems

Thermal control - QuickField simulation example

The bimetallic thermal control is made of a brass bar and magnesium bar. The bars are arranged so that there is the gap between their ends at room temperature.

Engineering question

How to find the contact temperature and thermal stress in a bimetallic thermal control?

Answer
Use LabelMover to raise the temperature until thermal expansion closes the gap, then solve the stress problem at the specified higher temperature after the bars are in contact.

More questions →

Typical applications
bimetal thermal switches, temperature control contacts, thermal expansion actuators

Thermal control

Download

Simulation problem

Problem Type
Axisymmetric problem of stress analysis

Geometry
Thermal control The bimetallic thermal control is made of a brass bar and magnesium bar. The bars are arranged so that there is the gap between their ends at room temperature brass magnesium Lb Lm δ

Given
Brass bar length Lb = 0.75";
Young's modulus of the brass Eb = 15·106 psi (103 GPa);
Thermal expansion coefficient of the brass αb = 10·10-6 1/°F (18·10-6 1/K);
Magnesium bar length Lm = 1.3";
Young's modulus of the magnesium Em = 6.5·106 psi (44.8 GPa);
Thermal expansion coefficient of the magnesium αm = 14.5·10-6 1/°F (26.1·10-6 1/K);
Initial distance between bars δ=0.005".

Task

  1. Calculate the temperature increase at which the two bars come into contact;
  2. Calculate the stress σ in the magnesium bar when the temperature increase is ΔT = 300 °F (167 K)

Solution
First part is solved using serial analysis capability of LabelMover. Temperatures of the bars rise with the step of 1 K. Elongation of the bars is calculated for each temperature. The bars come into contact when the total elongation of bars reaches δ. This way the temperature of the contact T1 is determined. There is no stress in the bars before the contact takes place.

The second part simulates bars after they came into contact. The deformed (elongated) bars geometry is used. In this problem the temperature increment T2 = ΔT - T1 is applied to the bars.

Results
Temperature at which the contact takes place: T1 = 106 K (191 °F)
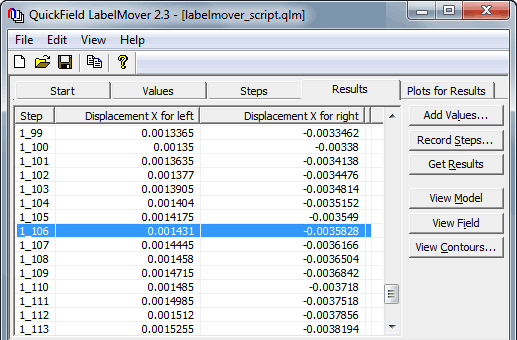
bimetallic thermal control parametric simulation

Thermal stress at temperature T2 = 300 - 191 = 109 °F (61 K).
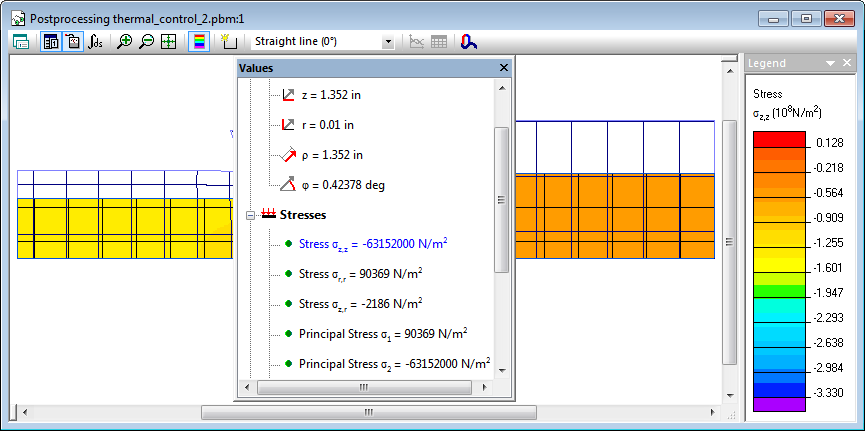
bimetallic thermal control mechanical stress

Contact temperature Stress in the magnesium
QuickField 191 °F (106 K) 9170 psi (63.2 MPa)
Theory* 190 °F 9680 psi
Difference 0.5% 6%

*James M. Gere, Stephen P. Timoshenko "Mechanics of materials", Third edition (1990), pp.26-27. ISBN: 0-534-92174-4.

Video

Related examples