Water liquid solid phase change
QuickField simulation example
Conversion of water to/from its solid form – ice – causes the phase transition and release of the internal energy called the latent heat of fusion.
In this example we simulate this conversion process of water already cooled to zero degrees [1]. To take into account the latent heat of fusion we modify the specific heat capacity vs. time dependency and add the artificial step. The area below the step corresponds to the latent heat of fusion.
Problem Type
Plane-parallel problem of transient heat transfer.
Geometry
Given
Task
Solution
To take into account the latent heat of fusion the nonlinear specific heat vs. temperature distribution is specified [2].
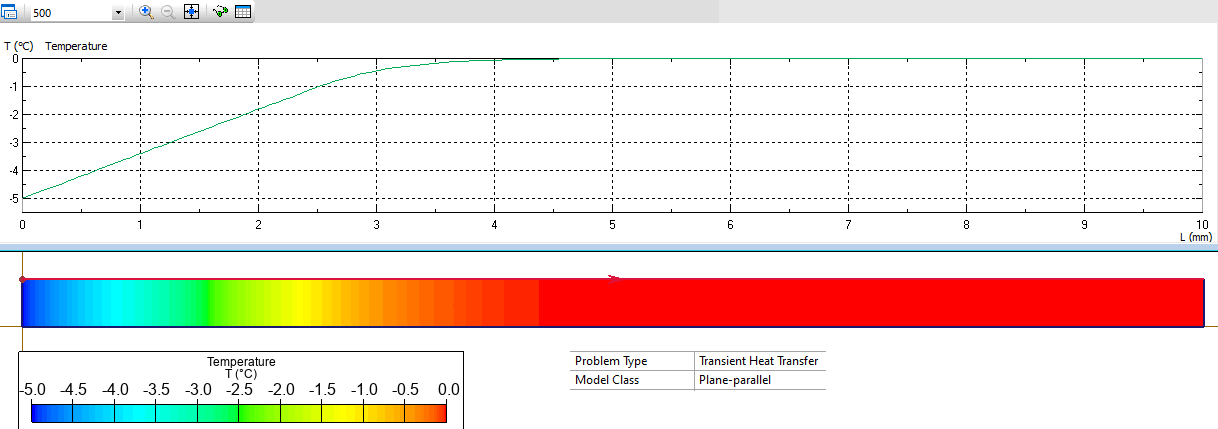
Results
References:
Water thermal conductivity 0.6 W/K-m, density ρ=1000 kg/m³, specific heat C = 4200 J/(kg*K).
Ice thermal conductivity 2.2 W/K-m, density ρ=910 kg/m³, specific heat C = 2100 J/(kg*K).
Latent heat of fusion Lf = 334 kJ/kg.
Calculate the temperature distribution in the ice.
The heat absorbed vs. temperature rise dynamics depends on the product of specific heat and the density ρ*C. For the ice it is 910*2100 = 1911 (kJ/K*m³). For the water it is 1000*4200 = 4200 (kJ/K*m³).
Latent heat of fusion we recalculate on a per volume basis using the water density: Lf*ρ = 334000 kJ /m³.
In QuickField we artificially set constant value of density ρ = 1000 kg/m³. It is considered that freezing occurs in the temperature interval ΔT from -0.5°C to +0.5°C. In this interval the specific heat value is C' = Lf*ρ / ΔT = 334 kJ/kg.
[1] ANSYS Mechanical APDL Verification Manual, example VM104. November 2013.
[2] Jonathan A. Dantzig, Modelling liquid–solid phase changes with melt convection, International Journal Numerical Methods in Engineering, 28 (8) 1989, pp. 1769-1785