Ampere's force law - QuickField simulation example

This verification example compares the force of attraction between two thin parallel current-currying wires given by Ampere's law and calculated in QuickField using three formulations: DC magnetics, time harmonics and transient magnetics.

Engineering question

How to find force between parallel current-carrying conductors?

Answer
Set up a plane-parallel QuickField DC Magnetics problem for a parallel conductor arrangement and evaluate force between current-carrying conductors from computed field results.

Download

Download simulation files (files may be viewed using any QuickField Edition).

Simulation problem

Problem Type
Plane-parallel problem of DC magnetics.

Geometry

Given
I = 1 A - current of each wire;
f = 50 Hz - frequency in time harmonics and transient magnetics problems;
R = 1 m - distance between the wires.

Task
Calculate interaction force (per meter of length) between two wires and compare with the value given by the Ampere's force law.

Solution
Currents are set as linear ones. This way the model completely corresponds to Ampere's formulation.
In the time harmonics problem peak amplitude value of current is set √2·I.
In the transient magnetics current is set via formula I(t) = √2·I · sin(2·180·50·t).

According to the Ampere's law^* the force of the interaction between two parallel wires is determined as:
f = 2·(μ₀/4π) · I·I / R [N/m]

Results
Ampere's law: f = 2·(μ₀/4π) · 1·1/ 1 = 2·10^-7 [N/m]

Magnetostatics: f = 2.00·10^-7 [N/m]
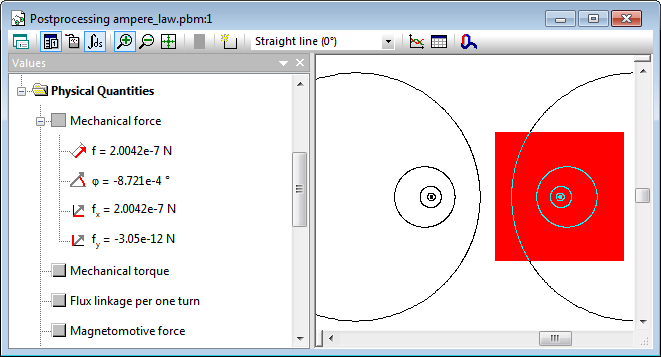
Ampere force in DC magnetics

Time harmonics: f = 2.00·10^-7 [N/m]
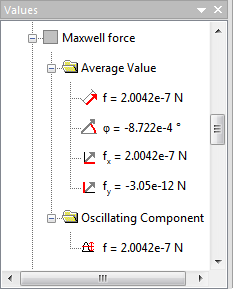
Ampere force in Time harmonics
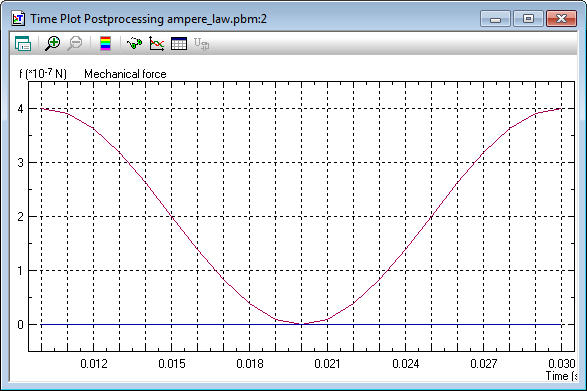
Transient magnetics: time-average force f = 2.00·10^-7 [N/m]