QuickField
A new approach to field modelling

Industrial

Educational

Scientific

Sample problems

Examples gallery

Step-by-step tutorials

Verification examples

Programming examples

Distributive examples

Success stories

Customers

Main >> Applications >> Sample problems >> Cable thermal conductivity

Cable thermal conductivity

QuickField simulation example

IEC 60287-2-1 [1] provides the method for calculation of the thermal resistance conductor to sheath of the cable. In this example we use a practical approach to simplify a cable structure and calculate the equivalent thermal resistance of the high voltage XLPE cable [2].

Problem Type
Plane-parallel problem of Heat transfer.

Geometry
Cable length is Lz = 1 km.
Two cable cross-sections are considered, original and simplified. Both models feature the same conductor diameter, external cable diameter and the sheath cross-section area.
Cable thermal conductivity Both original and simplified models feature the same conductor cross-section area and the sheath cross-section area. HDPE jacket Anti-corrosive layer Aluminum sheath Buffer layer Outer semi-conductive screen XLPE Inner semi-conductive screen Conductor SIMPLIFIED MODEL Conductor Dielectric Sheath Jacket Ø33.7 mm Ø33.7 mm Ø96.9 mm Ø96.9 mm 26.02 mm

Given
Conductor current is 800 A, frequency 50 Hz, resistance is 0.0321 Ohm/km.
Sheath current is 150 A. Aluminum sheath electric resistivity is 26.5 uOhm*mm, cross-section area is 157 mm².

ItemThermal conductivity [2],
W/K*m
Conductor (copper)402
Inner semi-conductive screen0.658
XLPE0.286
Outer semi-conductive screen0.491
Buffer layer
(water blocking strip and the air gap)		0.09
Aluminum sheath230
Anti-corrosive layer0.024
HDPE jacket2.28
Outer conductive screen0.41

Task
Calculate the equivalent thermal conductivity of the cable between the conductor and sheath.

Solution
Power loss in the conductor is Pconductor = Current² * Resistance = 800² * 0.0321 = 20.5 kW per 1 km of the cable length.
In QuickField we specify power density Qconductor = Pconductor / (Lz * Cross-section area) = 20500 / (1000 * π·0.0337²/4) = 23 kW/m³.

Electrical resistance of the sheath is R = electric resistivity * Lz / Cross-section area = 26.5e-9 * 1000 / 157e-6 = 0.169 Ohm/km.
Power loss in the sheath is Psheath = 150² * 0.169 = 3.8 kW/km.
In QuickField we specify power density Qsheath = Psheath / (Lz * Cross-section area) = 3800 / (1000 * 157e-6) = 24.2 kW/m³.

We specify temperature at the cable surface of +70°C and simulate the original model and calculate the temperature of the conductor.
Then we use the LabelMover tool to perform the optimization of the simplified model. The goal is to adjust thermal conductivity of the dielectric so that the conductor temperature matches the conductor temperature value calculated in the original model.

Results
Conductor surface temperature is 86.9°C. Equivalent thermal conductivity of the dielectric is λ = 0.182 W/(K·m).

Temperature distribution in the cables
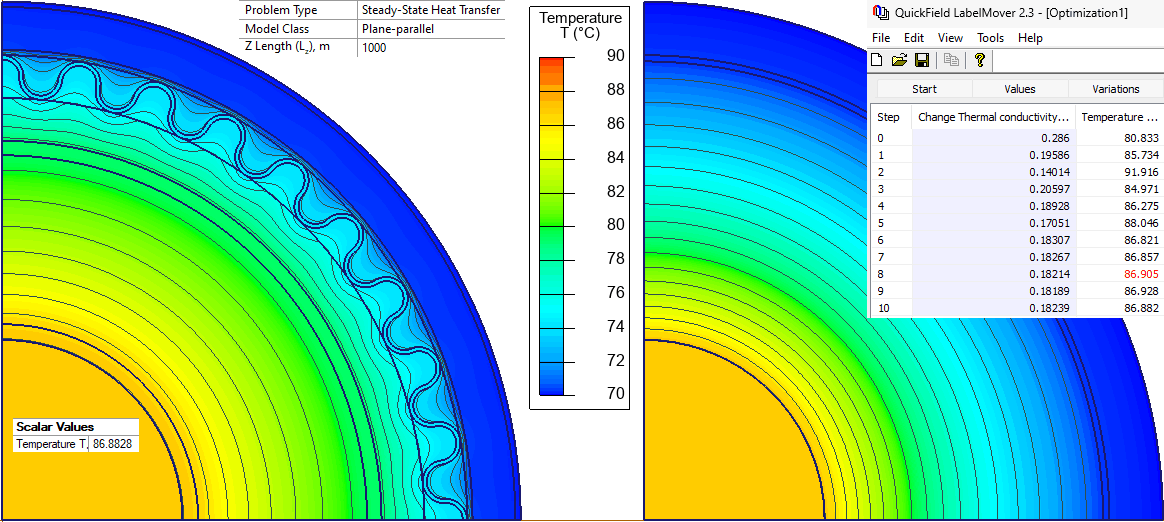
Cable thermal conductivity

Thermal resistance conductor to sheath = Temperature difference / Heat flux = (86.9 - 70.18) / 20.5 = 0.816 K*m/W.
It may be compared with the thermal resistance conductor to sheath calculated in accordance with IEC 60287-2-1: T1 = (1/λ/2/π) * LN(1 + 2*t/d) = (1/0.182/2/3.142) * LN(1 + 2*26.02/33.7) = 0.816 K*m/W.

References:
[1] IEC 60287-2-1 Electric cables - Calculation of the current rating - Part 2-1: Thermal resistance - Calculation of thermal resistance.
[2] Xin, Yue & Lei, Jiang & Zhao, Xiyuan & Li, Wenbin & Gao, Jinghui & Xi, Baofeng & Zhong, Lisheng & Xia, Linfeng., Cause Analysis of Aging Ablation on Sheath of 110 kV Single Core High Voltage Cable, 2019.