Electric circuit analysis
QuickField simulation example
QuickField offers an opportunity to include an electric circuit into the analyzed model. This example demonstrates the accuracy of the embedded circuit simulation.
Problem Type
Plane-parallel problem of AC Magnetics.
Geometry
As it is explained in the Solution section below, the field model geometry is not affecting the circuit simulation. Here is the circuit schema.
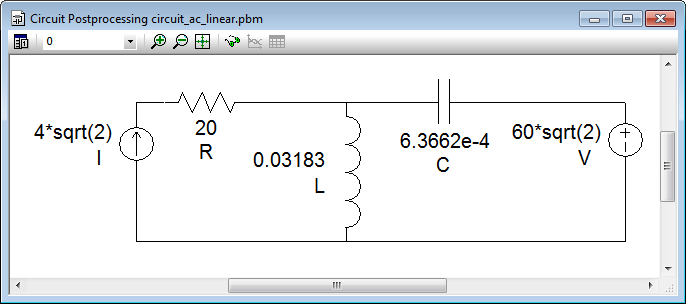
Given
R = 20 Ohm
XL = 10 Ohm
XC = 2 Ohm
Current source I = 4 A (RMS) @ 0°
Voltage source U = 60 V (RMS) @ 30°
Frequency f = 50 Hz
Task
Calculate currents and voltages in the circuit elements, check the power balance.
Solution
QuickField could solve only coupled field-circuit problems, and the field problem should be AC or Transient Magnetic. So we created fictitious AC Magnetic problem with one block, not connected to the circuit, just to agree with this requirement. All following considerations and results relate to the circuit simulation only.
Total power is determined as S = U * I' = P + i*Q,
where U - voltage [V],
I' - complex conjugate of current [A],
P - average active power [W],
Q - reactive power [V·Ar].
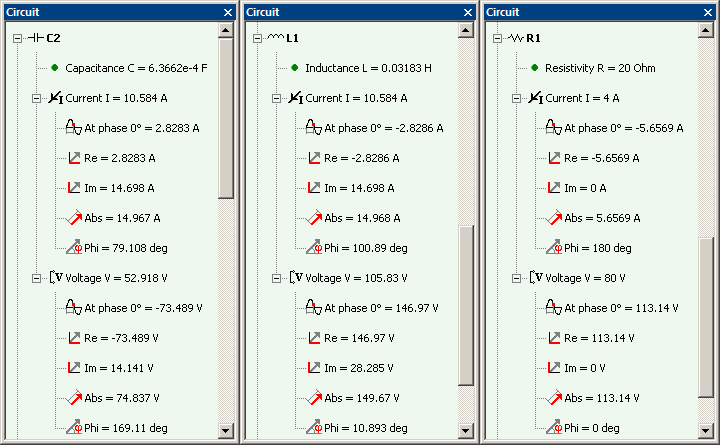
Results
Complex power in voltage source V
S(V) = 60@30° * 10.58@(-79.1°) = 634.8@(-49.1°) = 415.6 - i*479.8 [V·A].
Measured RMS values of voltages and currents, average values of powers.
| Voltage V, V | Current I, A | Real power P, W | Reactive power Q, V·Ar | |
| R | 80 @ 0° | 4 @ 180° | 320 | 0 |
| L | 105.8 @ 10.9° | 10.58 @ 100.9° | 0 | 1119.4 |
| C | 52.9 @ 169.1° | 10.58 @ 79.1° | 0 | -559.7 |
| V | 60 @ 30° | 10.58 @ -100.9° | 415.6 | -479.8 |
| I | 185 @ 6.2° | 4 @ 0° | -735.6 | -79.9 |
Power balance | 0 | 0 | ||
*Mathematical Methods for Physicists. A Comprehensive Guide. 7th Edition. George Arfken, Hans Weber, Frank Harris, p 937-938. ISBN 978-0-12-384654-9.
- Video: Electric circuit analysis. Watch on YouTube
- View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).