Temperature distribution in the conducting sheet

QuickField simulation example

The voltage is applied to the sides of conducting sheet placed vertically. The flowing current heats the sheet due to resistive losses. The front and back surfaces of the sheet are cooled by the air (natural convection).

Engineering question
How to find temperature rise in conducting sheets?

Engineering answer
Set up a plane-parallel QuickField Multiphysics problem for a conducting sheet and evaluate temperature rise from computed field results.

Typical applications
film heaters, fuse strips, conducting sheet heaters

• Download simulation files (files may be viewed using any QuickField Edition).

Problem Type
Plane-parallel multiphysics problem of DC conduction coupled to Heat Transfer.

Geometry

Given
Sheet thickness d = 1 mm;
Material conductivity σ = 1 MS/m;
Voltage applied U = 0.02 V;
Material heat conductivity λ = 50 W/K-m;
Convection coefficient α = 10 W/K-m²;
Ambient air temperature T₀ = 0°C.

Task
Calculate the current and temperature distribution in a conducting sheet.

Solution
The resistive losses are calculated in the DC conduction problem. Then these losses are transferred to the linked heat transfer problem.
All faces are washed by the air and subjected to the same cooling conditions:
Q [W/m²] = -α·T, where α - convection coefficient.
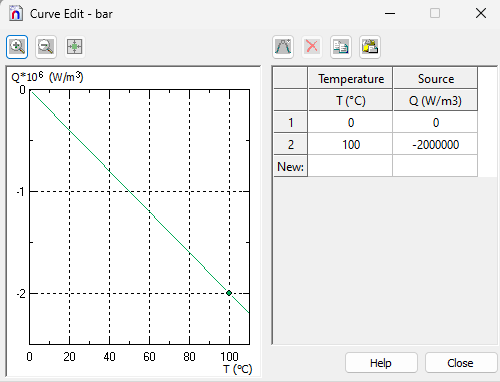
The convection from front and back faces is modelled by temperature depended heat sink
Q [W/m³] = - k·T, where k = 2 * α / d

Results
Current density and temperature distribution in the conducting sheet

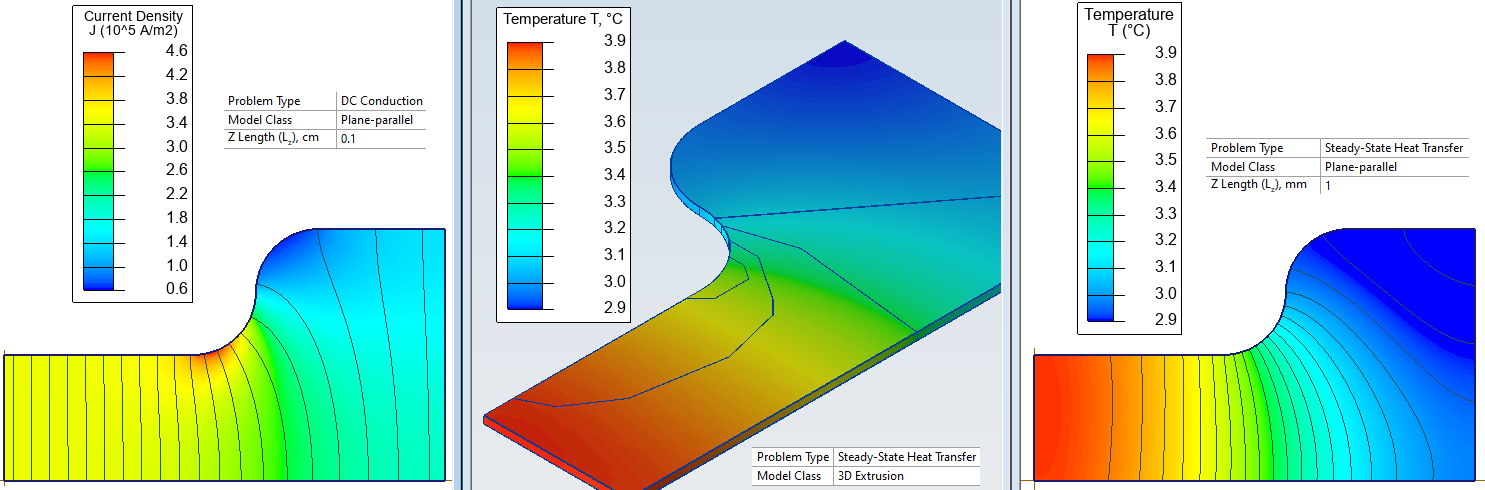
The Coupl5CF.pbm is the problem of calculating the current distribution in the sheet, and Coupl5HT.pbm analyzes temperature field.

• Video: Temperature distribution in the conducting sheet. Watch on YouTube
  
• Video: Temperature distribution in the conducting sheet. 3D. Watch on YouTube
  
• View simulation report in PDF