Main >> Applications >> Sample problems >> Temperature distribution in an electric wire
Temperature distribution in an electric wire
electric wire temperature distribution, heating of electric wire, multiphysics analysis
Calculate the temperature distribution in a long current carrying wire.
Problem Type
Axisymmetric multiphysics problem of DC Conduction coupled to Heat Transfer.
Geometry
Given
Wire diameter d = 0.75";
Resistance ρ = 9.35·10-8 Ohm/m;
Electric current I = 1000 A;
Thermal conductivity λ = 13 Btu·ft/(h·ft²·°F) = 22.5 W/(K·m);
Convection coefficient α = 5 Btu/(h·ft²°F) = 28.4 W/(K·m²);
Ambient temperature To = 70°F = 21.1°C.
Task
Calculate the temperature distribution in the wire.
Solution
We arbitrary chose a 1-foot (12") piece of wire to be represented by the model.
Material electric conductivity is σ = 1/ρ = 1/9.35e-8 = 10.7·106 S·m.
For the conduction problem we specify normal current density at one end j = I /(πd²/4) [A/m²] and zero voltage at another end of the wire, and a zero current condition at its surface.
For heat transfer problem we specify zero thermal flux conditions at the sections of the wire and a convection boundary condition at its surface.
Results
Temperature distribution in an electric wire:
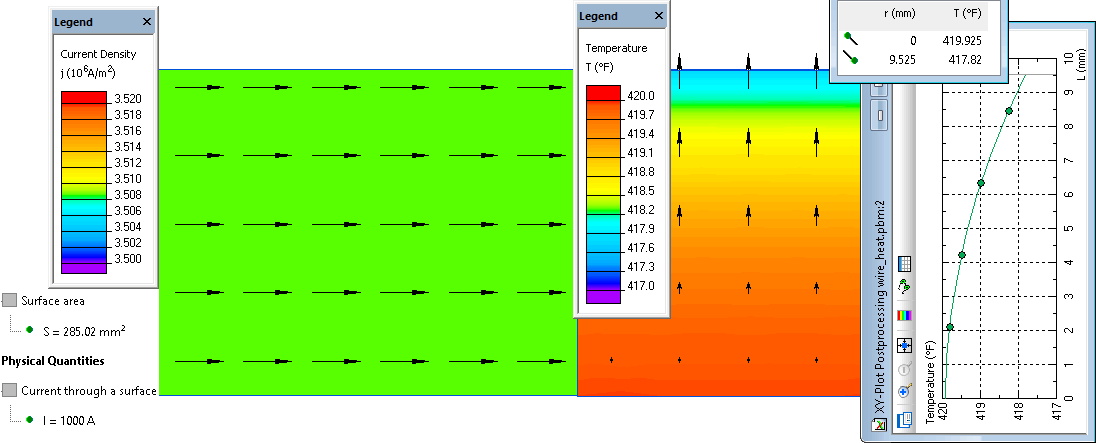
| Center line temperature | Surface temperature | |
| Theory | 419.9 F (215.5 °C) | 417.9 F (214.4 °C) |
|---|---|---|
| QuickField | 215.5 °C | 214.3 °C |
* Reference: W. Rohsenow and H. Y. Choi, "Heat, Mass, and Momentum Transfer", Prentice-Hall, N.J., 1963.
- Video: Temperature distribution in an electric wire
- View simulation report in PDF
- Download simulation files (files may be viewed using any QuickField Edition).
