Ferromagnetic particle force

QuickField simulation example

A small ferromagnetic particle is placed next to the circular current currying loop of wire.

Problem Type
Axisymmetric problem of DC magnetics

Geometry

Particle diameter 1 mm.

Given
I = 50 A - current in the wire;
μ = 1000 - relative magnetic permeability of the particle.

Task
Calculate the force acting on the particle placed at the axis of the ring as a function of the distance from the ring center.

Solution
Flux density distribution produced by the circular current could be calculated analytically. However, the particle causes local field distortion. Since the particle and ring feature cylindrical symmetry the model simulated as 2D axisymmetric. Axis of rotation is horizontal one.
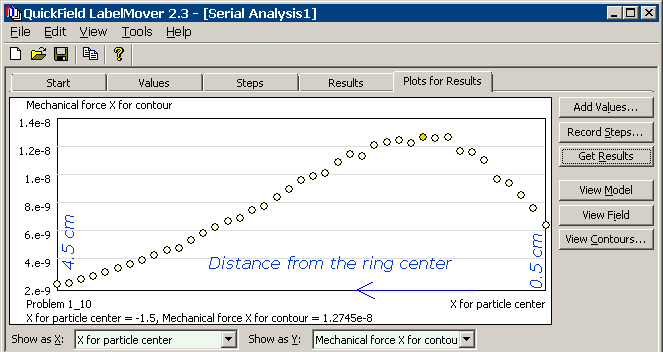
LabelMover tool is used to automate the force vs. distance dependency calculation.

Results
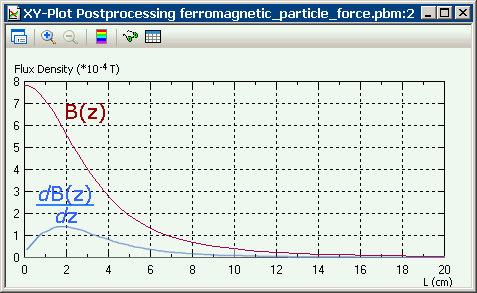
Flux density B(z) peak value is 0.78 mT (located at the ring center)
Flux density gradient dB(z)/dz peak value is 17 mT/m (located 2 cm away from the ring center)

Flux density B(z) and gradient dB(z)/dz distribution along the ring axis:

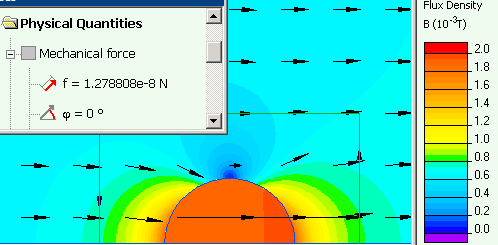
Magnetic field distortion caused by the ferromagnetic particle.

Force acting on a particle as a function of distance from the ring center:

• Download simulation files (files may be viewed using any QuickField Edition).