Natural convection from the inclined plate surface
QuickField simulation example
Inclined steel plate release its heat to the environment.
Problem Type
Plane-parallel problem of steady-state heat transfer.
Geometry
Length of the plate L = 1000 mm, thickness of the plate d = 2 mm, angle of slope θ = 50°.
Given
Temperature of the lower surface of the plate T0 = 20 °C,
Temperature of the air above the plate T = -10 °C
Thermal conductivity of the plate λplate = 0.4 W/(m·K)
Task
Calculate the temperature of the upper surface of the plate and the heat flux passing through the surface.
Solution
Lower surface of the plate is heated to the 20 °C and the air temperature above the upper surface is -10 °C so that the heat flux inside the plate is directed to the upper surface. Upper surface of the plate is hotter than the surrounding air so that the heat flux of natural convection is directed to the cold environment. We estimate that the temperatures of the upper plate surface is equal to the temperature of the lower plate surface
Tupper = T0 = 20 °C.
This value is used for the convection coefficient calculation*:
αupper = 4 W/(m²·K).
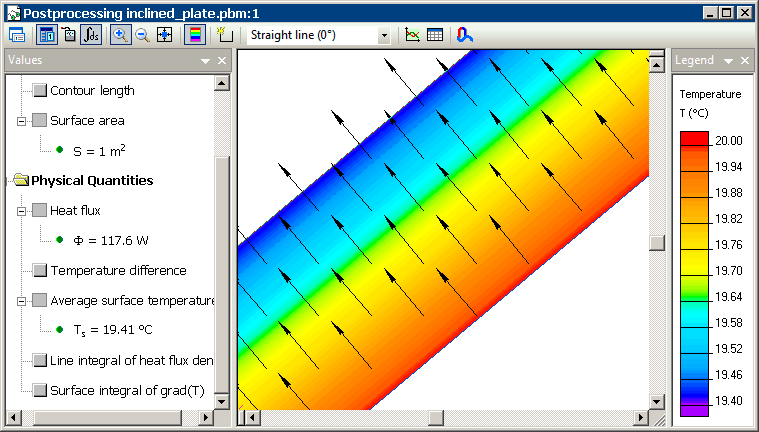
Result
Temperature of the upper surface of the plate: Tupper = 19.4 °C.
Heat flux: f = 117 W (plate surface area is 1 m²).
*Remark: the formulas of the similarity theory relate to the big plates and gives the average value of the convection coefficient. This approach is very approximate by its nature, so there is no reason to make iterations to calculate the accurate convection coefficient value related to actual surfaces temperatures.
- View simulation report in PDF.
- Download simulation files (files may be viewed using any QuickField Edition).