Customers

Publications

Site map

   A new approach to field modelling

Applications>

Sample problems 

Coupl2: Pipe subject to temperature and pressure

A very long, thick-walled cylinder pipe is subjected to an internal pressure and a steady state temperature distribution with T_i and T_o temperatures at inner and outer surfaces respectively. Calculate the stress distribution in the cylinder.

Problem Type:

Axisymmetric problem of thermo-structural coupling.

Geometry:

Given:

Dimensions R1 = 1 cm, R2 = 2 cm;
Inner surface temperature T_i = 100 °C;
Outer surface temperature T_o = 0 °C;
Coefficient of thermal expansion α = 10 ^-6 1/K;
Internal pressure P = 10⁶ N/m²;
Young's modulus E = 3·10¹¹ N/m²;
Poisson's ratio ν = 0.3.

Problem:

Calculate the stress distribution in the pipe.

Solution:

Since none of physical quantities varies along z-axis, a thin slice of the cylinder can be modeled. The axial length of the model is arbitrarily chosen to be 0.2 cm. Axial displacement is set equal to zero at the side edges of the model to reflect the infinite length of the cylinder.

Comparison of Results

Temperature distribution in cylinder pipe:	Stress distribution in a cylinder pipe:

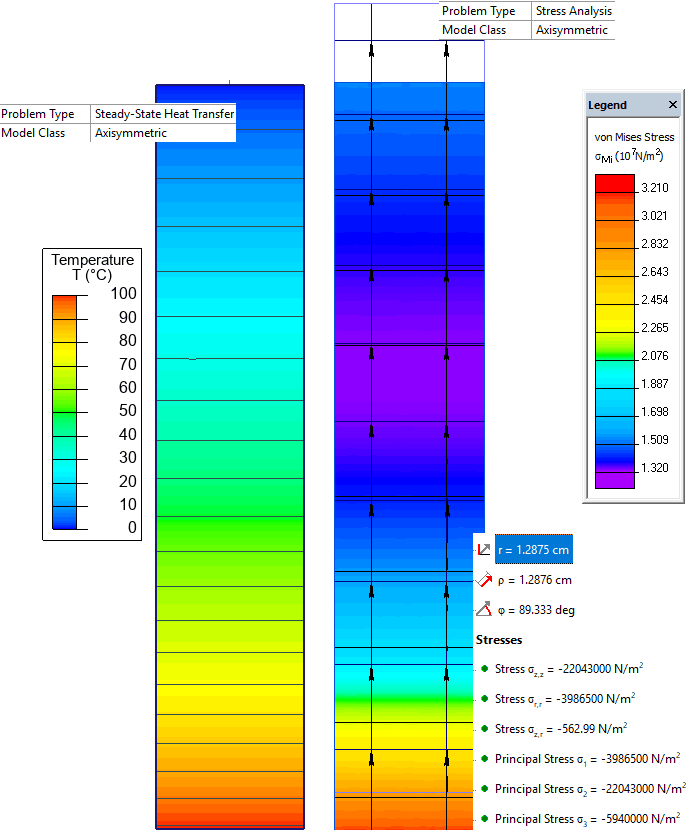
Radial and circumferential stress at r=1.2875 cm:

	σr (N/m2)	σq (N/m2)
Theory	-3.9834·106	-5.9247·106
QuickField	-3.959·106	-5.924·106

See the Coupl2HT.pbm and Coupl2SA.pbm problems are for the corresponding heat transfer and structural analysis.

Reference

S. P. Timoshenko and Goodier, "Theory of Elasticity", McGraw-Hill Book Co., N.Y., 1961, pp. 448-449.

Download simulation files:

for Student edition	for Professional edition
coupl2_stud.zip	coupl2.zip